
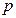 。
。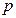 的取值范围;
的取值范围;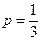 ,当采用3局2胜制的比赛规则时,求甲获胜的概率;
,当采用3局2胜制的比赛规则时,求甲获胜的概率;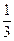 吗?
吗? 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
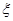 的分布列和数学期望;
的分布列和数学期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| A1 | A2 | A3 | A4 | A5 |
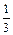 ,为1的概率为
,为1的概率为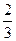 .例如若A=10001,其中A1= A5=1,A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时,
.例如若A=10001,其中A1= A5=1,A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时,查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 3 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.2 | B.0.3 |
| C.0.4 | D.0.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com