
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)已知![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】对于函数f(x),若a,b,c∈R,f(a),f(b),f(c)都是某一三角形的三边长,则称f(x)为“可构造三角形函数”.以下说法正确的是( )
A.f(x)=1(x∈R)不是“可构造三角形函数”
B.“可构造三角形函数”一定是单调函数
C.f(x)=![]() 是“可构造三角形函数”
是“可构造三角形函数”
D.若定义在R上的函数f(x)的值域是![]() (e为自然对数的底数),则f(x)一定是“可构造三角形函数”
(e为自然对数的底数),则f(x)一定是“可构造三角形函数”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且此抛物线的准线被椭圆
的焦点重合,且此抛物线的准线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 是线段
是线段![]() 的垂直平分线,试问直线
的垂直平分线,试问直线![]() 是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一批零件,为了解这批零件的质量状况,检验员从这批产品中随机抽取了100件作为样本进行检测,将它们的重量(单位:g)作为质量指标值,由检测结果得到如下频率分布表和频率分布直方图.
分组 | 频数 | 频率 |
| 8 | |
| ||
| ||
| 16 | 0.16 |
| 4 | 0.04 |
合计 | 100 | 1 |
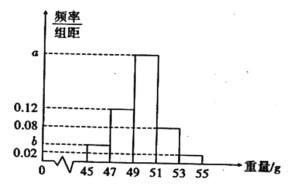
(1)求图中![]() ,
,![]() 的值;
的值;
(2)根据质量标准规定:零件重量小于47或大于53为不合格品,重量在区间![]() 和
和![]() 内为合格品,重量在区间
内为合格品,重量在区间![]() 内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该批零件重量的概率分布.若这批零件共400件,现有两种销售方案:
内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该批零件重量的概率分布.若这批零件共400件,现有两种销售方案:
方案一:对剩余零件不再进行检测,回收处理这100件样本中的不合格品,余下所有零件均按150元/件售出;
方案二:继续对剩余零件的重量进行逐一检测,回收处理所有不合格品,合格品按150元/件售出,优质品按200元/件售出.
仅从获得利润大的角度考虑,该生产商应选择哪种方案?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() ,
,![]() 及函数
及函数![]() (
(![]() ),
),![]() (
(![]() ).
).
(1)若等比数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() (
(![]() )项和;
)项和;
(2)已知等差数列![]() 满足
满足![]() ,
,![]() ,
,![]() (
(![]() 、
、![]() 均为常数,
均为常数,![]() ,且
,且![]() ),
),![]() (
(![]() ).试求实数对(
).试求实数对(![]() ,
,![]() ),使得
),使得![]() 成等比数列.
成等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com