
���� ��1��b1=a1+a2=3���ɵ�bn=3n=a2n-1+a2n�����÷��������ȱ����е����ʽ���ɵó�S2n��
��2��������n��N*��Sn=$\frac{{a}_{n}^{2}+n}{2}$��������ɵ�n��2ʱ��an=Sn-Sn-1����Ϊ��$��{a}_{n}-1��^{2}$=${a}_{n-1}^{2}$��an��0���ɵ�an-an-1=1�����õȲ����е�ͨ�ʽ���ɵó���
��3����S2n=3��2n-1������a1=1��a2=2���ɵ�a1+a2+a3+a4=9���ɵ�a3+a4=6��������{anan+1}ҲΪ�ȱ����У��蹫��Ϊq=$\frac{{a}_{n+2}}{{a}_{n}}$���ɵ�����{an}����������ż����ֱ�ɵȱ����У�����Ϊq�����ɵó���
��� �⣺��1��b1=a1+a2=3����bn=3n=a2n-1+a2n��
��S2n=3+32+��+3n=$\frac{3��{3}^{n}-1��}{3-1}$=$\frac{{3}^{n+1}-3}{2}$��
��2��������n��N*��Sn=$\frac{{a}_{n}^{2}+n}{2}$�������
��n��2ʱ��an=Sn-Sn-1=$\frac{{a}_{n}^{2}+n}{2}$-$\frac{{a}_{n-1}^{2}+n-1}{2}$����Ϊ��$��{a}_{n}-1��^{2}$=${a}_{n-1}^{2}$��an��0��
��an-1=an-1����an-an-1=1��
��an=1+��n-1��=n��
��3����S2n=3��2n-1������a1=1��a2=2��
��a1+a2+a3+a4=3����22-1��=9=1+2+a3+a4��
��a3+a4=6��
������{anan+1}ҲΪ�ȱ����У��蹫��Ϊq=$\frac{{a}_{n+2}}{{a}_{n}}$��
������{an}����������ż����ֱ�ɵȱ����У�����Ϊq��
��a3=q��a4=a2q=2q��
��q+2q=3��2�����q=2��
��${a}_{2n-1}={a}_{1}{q}^{n-1}$=2n-1��
a2n=${a}_{2}{q}^{n-1}$=2n��
�ɵ�an=$\left\{\begin{array}{l}{{2}^{\frac{n-1}{2}}��n=2k-1}\\{{2}^{\frac{n}{2}}��n=2k}\end{array}\right.$��k��N*����
���� ���⿼�������е��ƹ�ϵ���Ȳ�������ȱ����еĶ���ͨ�ʽ�����ʽ�������˷������۷�������������������������������⣮


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
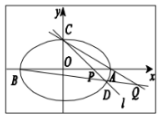 ����C��0��$\sqrt{2}$������Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{2}}{2}$����Բ��x�ύ������A��a��0����B��-a��0��������C��ֱ��l����Բ������һ��D������x�ύ�ڵ�P��ֱ��AC��BD���ڵ�Q��
����C��0��$\sqrt{2}$������Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{2}}{2}$����Բ��x�ύ������A��a��0����B��-a��0��������C��ֱ��l����Բ������һ��D������x�ύ�ڵ�P��ֱ��AC��BD���ڵ�Q���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 6 | C�� | 8 | D�� | 1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com