
【题目】已知数列{bn}满足bn=| ![]() |,其中a1=2,an+1=
|,其中a1=2,an+1= ![]()
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)设cn= ![]() ,数列|cn|的前项和为Sn , 求证Sn<
,数列|cn|的前项和为Sn , 求证Sn< ![]() .
.
【答案】
(1)解:由a1=2,an+1= ![]() 可得:a2=
可得:a2= ![]() ,a3=
,a3= ![]() .又bn=|
.又bn=| ![]() |,
|,
则b1=4,b2=8,b3=16.
猜想bn=4×2n﹣1=2n+1
(2)解:证明:cn= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴数列|cn|的前项和为Sn= ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() .
.
∴Sn< ![]()
【解析】(1)由a1=2,an+1= ![]() 可得:a2=
可得:a2= ![]() ,a3=
,a3= ![]() .又bn=|
.又bn=| ![]() |,可得b1 , b2 , b3 . 猜想bn=2n+1 . (2)cn=
|,可得b1 , b2 , b3 . 猜想bn=2n+1 . (2)cn= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,即可得出数列|cn|的前项和为Sn .
,即可得出数列|cn|的前项和为Sn .
【考点精析】掌握数列的定义和表示和数列的前n项和是解答本题的根本,需要知道数列中的每个数都叫这个数列的项.记作an,在数列第一个位置的项叫第1项(或首项),在第二个位置的叫第2项,……,序号为n的项叫第n项(也叫通项)记作an;数列{an}的前n项和sn与通项an的关系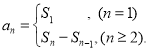 .
.


科目:高中数学 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 25 | a | b |
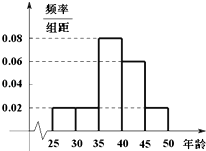
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果 ![]() ,
, ![]() 是平面
是平面 ![]() 内所有向量的一组基底,那么( )
内所有向量的一组基底,那么( )
A.若实数 ![]() ,
, ![]() ,使
,使 ![]() ,则
,则 ![]()
B.空间任一向量 ![]() 可以表示为
可以表示为 ![]() ,这里
,这里 ![]() ,
, ![]() 是实数
是实数
C.![]() ,
, ![]() 不一定在平面
不一定在平面 ![]() 内
内
D.对平面 ![]() 内任一向量
内任一向量 ![]() ,使
,使 ![]() 的实数
的实数 ![]() ,
, ![]() 有无数对
有无数对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:在数列 ![]() 中,若
中,若 ![]()
![]() 为常数)则称
为常数)则称 ![]() 为“等方差数列”,下列是对“等方差数列”的有关判断( )
为“等方差数列”,下列是对“等方差数列”的有关判断( )
①若 ![]() 是“等方差数列”,在数列
是“等方差数列”,在数列 ![]() 是等差数列;
是等差数列;
② ![]() 是“等方差数列”;
是“等方差数列”;
③若 ![]() 是“等方差数列”,则数列
是“等方差数列”,则数列 ![]() 为常)也是“等方差数列”;
为常)也是“等方差数列”;
④若 ![]() 既是“等方差数列”又是等差数列,则该数列是常数数列.
既是“等方差数列”又是等差数列,则该数列是常数数列.
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的焦距为2
=1(a>b>0)的焦距为2 ![]() ,椭圆C上任意一点到椭圆两个焦点的距离之和为6. (Ⅰ)求椭圆C的方程;
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=kx﹣2与椭圆C交于A,B两点,点P(0,1),且|PA|=|PB|,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=xlnx有如下结论: ①该函数为偶函数;
②若f′(x0)=2,则x0=e;
③其单调递增区间是[ ![]() ,+∞);
,+∞);
④值域是[ ![]() ,+∞);
,+∞);
⑤该函数的图象与直线y=﹣ ![]() 有且只有一个公共点.(本题中e是自然对数的底数)
有且只有一个公共点.(本题中e是自然对数的底数)
其中正确的是(请把正确结论的序号填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com