
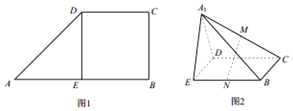
 如图1.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AEDD折起到△A1ED的位置,连结A1B,A1C,M,N分别为A1C,BE的中点.如图2.
如图1.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AEDD折起到△A1ED的位置,连结A1B,A1C,M,N分别为A1C,BE的中点.如图2.分析 (Ⅰ)推导出DE⊥A1E,DE⊥BE,从而DE⊥平面A1BE,由此能证明DE丄A1B.
(Ⅱ)取CD中点E,连结NE,ME,推导出平面A1DE∥平面MNE,由此能证明MN∥平面A1ED.
(Ⅲ)取A1B的中点G,连结EG,推导出EG⊥A1B,EG⊥BC,从百求出棱A1B上存在中点G.使得EG丄平面A1BC,此时$\frac{{A}_{1}G}{GB}$=1.
解答 证明:(Ⅰ)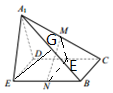 ∵在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,
∵在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,
沿DE将△AEDD折起到△A1ED的位置,
∴DE⊥A1E,DE⊥BE,
∵A1E∩BE=E,∴DE⊥平面A1BE,
∵A1B?平面A1BE,∴DE丄A1B.
(Ⅱ)取CD中点E,连结NE,ME,
∵M,N分别为A1C,BE的中点,
∴ME∥A1D,NE∥DE,
又DE∩A1D=D,NE∩ME=E,DE,A1D?平面A1DE,NE,ME?平面MNE,
∴平面A1DE∥平面MNE.
∴MN∥平面A1ED.
(Ⅲ)取A1B的中点G,连结EG,
∵A1E=BE,∴EG⊥A1B,
由(Ⅰ)知DE⊥平面A1BE,∵DE∥BC,∴BC⊥平面A1BE,
∴EG⊥BC,
又A1B∩BC=B,∴EG⊥平面A1BC.
故棱A1B上存在中点G.使得EG丄平面A1BC,此时$\frac{{A}_{1}G}{GB}$=1.
点评 本题考查线线垂直的证明,考查线面平行的证明,考查满足线面垂直的点的位置的确定与求法,考查推理论证能力、运算求解能力、空间想象能力,考查转化化归思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | A与B | B. | B与C | C. | A与D | D. | C与D |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{2}})∪[{\frac{1}{2},1}]$ | B. | $[{\frac{1}{2},1}]$ | C. | (0,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
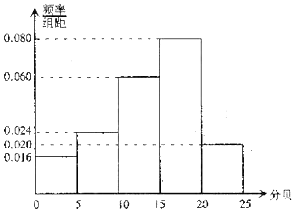 人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com