
已知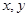 都是正数,
都是正数,
(1)若 ,求
,求 的最大值
的最大值
(2)若 ,求
,求 的最小值.
的最小值.
(1)6;(2)36.
【解析】
试题分析:(1)直接利用基本不等式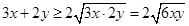 ,
, 的最大值随之而定;(2)如果直接利用基本不等式则有
的最大值随之而定;(2)如果直接利用基本不等式则有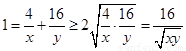 ①,
①, ,因此
,因此 ②,这样就可能得出
②,这样就可能得出 的最小值为32,实际上这个最小值是取不到的,因为不等式①取等号的条件是
的最小值为32,实际上这个最小值是取不到的,因为不等式①取等号的条件是 ,
, ,不等式②取等号的条件是
,不等式②取等号的条件是 ,即不等式①②不能同时取等号,故
,即不等式①②不能同时取等号,故 的最小值不是32.正确的解法是把
的最小值不是32.正确的解法是把 看作
看作 ,把其中的1用已知
,把其中的1用已知 代换,即
代换,即 ,展开后就可以直接利用基本不等式求出结果.
,展开后就可以直接利用基本不等式求出结果.
试题解析:(1)xy=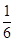 ·3x·2y≤
·3x·2y≤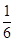
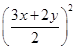 2=6
4分
2=6
4分
当且仅当 即
即 时取“=”号.
时取“=”号.
所以当x=2,y=3时,xy取得最大值6 ..6分
(2)由 且
且 得
得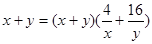
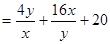
 , 10分
, 10分
当且仅当 ,即x=12且y=24时,等号成立,
,即x=12且y=24时,等号成立,
所以x+y的最小值是36 12分
考点:基本不等式的应用.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源:2011-2012学年江苏省苏北四市(徐、连、淮、宿)高三元月调研测试数学试卷 题型:解答题
选修4-5:不等式选讲(本小题满分10分)已知 都是正数,且
都是正数,且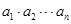 =1,求证:
=1,求证: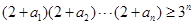
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三第二次月考理科数学试卷 题型:选择题
给出下列命题,其中正确命题的个数是( )
①已知 都是正数,
都是正数, ,则
,则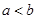 ;②
;②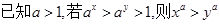 ;
;
③“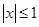 ,且
,且 ”是“
”是“ ”的充分不必要条件;
”的充分不必要条件;
④命题“ ,使得
,使得 ”的否定是“
”的否定是“ ,使得
,使得 ”.
”.
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com