
【题目】某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共![]() 层,总开发费用为
层,总开发费用为![]() 万元,求函数
万元,求函数![]() 的表达式(总开发费用=总建筑费用+购地费用);
的表达式(总开发费用=总建筑费用+购地费用);
(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意的
项和,若对任意的![]() ,不等式
,不等式![]() 都成立,求实数
都成立,求实数![]() 的取值范围;
的取值范围;
(3)记![]() ,是否存在互不相等的正整数
,是否存在互不相等的正整数![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,且
成等差数列,且![]() ,
,![]() ,
,![]() 成等比数列?如果存在,求出所有符合条件的
成等比数列?如果存在,求出所有符合条件的![]() ,
,![]() ,
,![]() ;如果不存在,请说明理由.
;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() ,点
,点![]() ,动圆
,动圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() (
(![]() 均不同于点
均不同于点![]() ),且
),且![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)证明:![]() 为定值,并求
为定值,并求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,当
两点,当![]() 三点共线时,求四边形
三点共线时,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,梯形![]() 中,
中,![]() ,过
,过![]() 分别作
分别作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.![]() ,
,![]() ,已知
,已知![]() ,将梯形
,将梯形![]() 沿
沿![]() ,
,![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2.
,如图2.
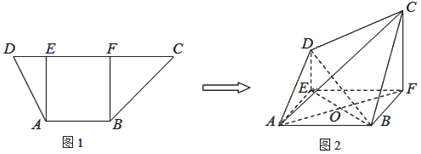
(1)若![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(2)在(1)的条件下,若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业在“精准扶贫”行动中,决定帮助一贫困山区将水果运出销售.现有8辆甲型车和4辆乙型车,甲型车每次最多能运6吨且每天能运4次,乙型车每次最多能运10吨且每天能运3次,甲型车每天费用320元,乙型车每天费用504元.若需要一天内把180吨水果运输到火车站,则通过合理调配车辆运送这批水果的费用最少为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() ,都有
,都有![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“L函数”.
为“L函数”.
(1)试判断函数![]() 与
与![]() 是否是“L函数”;
是否是“L函数”;
(2)若函数![]() 为“L函数”,求实数a的取值范围;
为“L函数”,求实数a的取值范围;
(3)若函数![]() 为“L函数”,且
为“L函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(﹣1,0)上与函数f(x)的单调性相同的是( )

A.![]() B.y=log2|x|
B.y=log2|x|
C. D.y=cos(2x)
D.y=cos(2x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com