
【题目】已知函数![]() ,
, ![]() .
.
(1)证明: ![]() ;
;
(2)根据(1)证明: ![]() .
.
(B)已知函数![]() ,
, ![]() .
.
(1)用分析法证明: ![]() ;
;
(2)证明: ![]() .
.
【答案】(A)(1)详见解析;(2)详见解析. (B)(1)详见解析;(2)详见解析.
【解析】试题分析:(A)(1)要证原不等式成立,先将函数的表达式代入原不等式,两边乘以![]() ,可以得到一个显然成立的结论,由此证得原不等式成立.(2)利用(1)的结论,将(1)右边的二次函数配方,求出其最小值,由此可证得
,可以得到一个显然成立的结论,由此证得原不等式成立.(2)利用(1)的结论,将(1)右边的二次函数配方,求出其最小值,由此可证得![]() ,而
,而![]() ,综上所述,
,综上所述, ![]() .(B)(1)(1)要证原不等式成立,先将函数的表达式代入原不等式,两边乘以
.(B)(1)(1)要证原不等式成立,先将函数的表达式代入原不等式,两边乘以![]() ,可以得到一个显然成立的结论,由此证得原不等式成立.(2)由于
,可以得到一个显然成立的结论,由此证得原不等式成立.(2)由于![]() 时,有
时,有![]() ,所以
,所以![]() ,令
,令![]() ,利用导数求得
,利用导数求得![]() 的最大值为
的最大值为![]() ,由此证得
,由此证得![]() .
.
试题解析:
(A)解(1)由![]() 有
有![]() ,
,
要证![]() ,
,
只需证![]() ,
,
只需证![]() ,
,
只需证![]() ,因为
,因为![]() 成立,所以
成立,所以![]() 成立.
成立.
(2)因为![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
又![]() ,
,
所以由(1)得![]() .
.
(B)解(1)由![]() 有
有![]() ,
,
要证![]() ,
,
只需证![]() ,
,
只需证![]() ,
,
只需证![]() ,因为
,因为![]() 成立,所以
成立,所以![]() 成立.
成立.
(2)证法1 由![]() 得
得![]() ,
,
则![]() ,
,
设![]() ,
, ![]() ,
,
则 ,
,
则![]() 在
在![]() 上为增函数,
上为增函数,
则![]() ,
,
所以![]() .
.
证法2 由![]() 有
有![]() ,
,
设![]() ,
, ![]() ,则
,则![]() ,设
,设![]() ,
,
则![]() ,
,
∵![]() ,∴
,∴![]() ,则
,则![]() 在
在![]() 时为增函数,
时为增函数,
又![]() ,
, ![]() ,
,
∴存在![]() ,使得
,使得![]() ,即
,即![]() ,
,
∴![]() 时,
时, ![]() 为减函数,
为减函数, ![]() 时,
时, ![]() ,
, ![]() 为增函数,
为增函数,
由![]() ,
, ![]() 有
有![]() 时,
时, ![]() 有最大值0,即
有最大值0,即![]() 成立.
成立.
则![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响,已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数![]() 为
为![]() 上的偶函数”为事件
上的偶函数”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司拟投资开发某项新产品,市场评估能获得10~1 000万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不低于1万元,同时不超过投资收益的20%.
(1) 设奖励方案的函数模型为f(x),试用数学语言表述公司对奖励方案的函数模型f(x)的基本要求;
(2) 公司能不能用函数f(x)=![]() +2作为预设的奖励方案的模型函数?
+2作为预设的奖励方案的模型函数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]()
![]() 的离心率为
的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(1) 求椭圆![]() 的方程;
的方程;
(2) 设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如下图所示,其中主视图与左视图是腰长为6的等腰直角三角形,俯视图是正方形.

(Ⅰ)请画出该几何体的直观图,并求出它的体积;
(Ⅱ)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1? 如何组拼?试证明你的结论;
(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
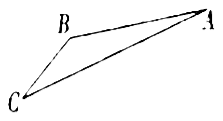
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:指数函数y=(1-a)x是R上的增函数,命题q:不等式ax2+2x-1>0有解.若命题p是真命题,命题q是假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com