
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小1.
的距离小1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() (2)过定点
(2)过定点![]() ,(3)4
,(3)4
【解析】试题分析:(Ⅰ)先借助抛物线定义确定曲线的形状是抛物线,再确定参数![]() ,进而求出
,进而求出![]() ;(Ⅱ)先依据(Ⅰ)的结论分别建立
;(Ⅱ)先依据(Ⅰ)的结论分别建立![]() 的方程,再分别与抛物线联立方程组,求出弦中点为
的方程,再分别与抛物线联立方程组,求出弦中点为![]() 的坐标,最后借助斜率的变化确定直线
的坐标,最后借助斜率的变化确定直线![]() 经过定点;(Ⅲ)在(Ⅱ)前提条件下,先求出
经过定点;(Ⅲ)在(Ⅱ)前提条件下,先求出![]() ,然后建立
,然后建立![]() 面积关于变量
面积关于变量![]() 的函数
的函数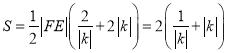 ,再运用基本不等式求其最小值:
,再运用基本不等式求其最小值:
解:(Ⅰ)由题意可知:动点![]() 到定点
到定点![]() 的距离等于
的距离等于![]() 到定直线
到定直线![]() 的距离.根据抛物线的定义可知,点
的距离.根据抛物线的定义可知,点![]() 的轨迹
的轨迹![]() 是抛物线.
是抛物线.
∵![]() ,∴抛物线方程为:
,∴抛物线方程为: ![]()
(Ⅱ)设![]() 两点坐标分别为
两点坐标分别为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
由题意可设直线![]() 的方程为
的方程为![]() .
.
由 ,得
,得![]() .
.
![]() .
.
因为直线![]() 与曲线
与曲线![]() 于
于![]() 两点,所以
两点,所以![]() .
.
所以点![]() 的坐标为
的坐标为![]() .
.
由题知,直线![]() 的斜率为
的斜率为![]() ,同理可得点
,同理可得点![]() 的坐标为
的坐标为![]() .
.
当![]() 时,有
时,有![]() ,此时直线
,此时直线![]() 的斜率
的斜率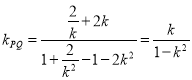 .
.
所以,直线![]() 的方程为
的方程为![]() ,整理得
,整理得![]() .
.
于是,直线![]() 恒过定点
恒过定点![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,也过点
,也过点![]() .
.
综上所述,直线![]() 恒过定点
恒过定点![]() .
.
(Ⅲ)可求得![]() .所以
.所以![]() 面积
面积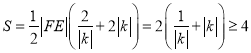 .
.
当且仅当![]() 时,“
时,“![]() ”成立,所以
”成立,所以![]() 面积的最小值为4.
面积的最小值为4.


科目:高中数学 来源: 题型:
【题目】已知集合A=[2,log2t],集合B={x|y= ![]() },
},
(1)对于区间[a,b],定义此区间的“长度”为b﹣a,若A的区间“长度”为3,试求实数t的值.
(2)若AB,试求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A.命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2≠0”
B.若p∧q为假命题,则p,q均为假命题
C.对命题P:存在x∈R,使得x2+x+1<0,则¬p为:任意x∈R,均有x2+x+1≥0
D.“x>2”是“x2﹣3x+2>0”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
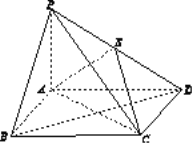
【题目】(本题满分12分)如图13,四棱锥P ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设AP=1,AD=![]() ,三棱锥P ABD的体积V=
,三棱锥P ABD的体积V=![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分) 已知集合![]() 在平面直角坐标系中,点M的坐标为(x,y) ,其中
在平面直角坐标系中,点M的坐标为(x,y) ,其中![]() 。
。
(1)求点M不在x轴上的概率;
(2)求点M正好落在区域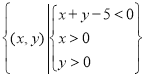 上的概率。
上的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“两个分厂生产的零件的质量有差异”.
的把握认为“两个分厂生产的零件的质量有差异”.
甲 厂 | 乙 厂 | 合计 | |
优质品 | |||
非优质品 | |||
合计 |
附: 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出三种函数模型:f(x)=xn(n>0),g(x)=ax(a>1)和h(x)=logax(a>1).根据它们增长的快慢,则一定存在正实数x0 , 当x>x0时,就有( )
A.f(x)>g(x)>h(x)
B.h(x)>g(x)>f(x)
C.f(x)>h(x)>g(x)
D.g(x)>f(x)>h(x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com