
【题目】在正项等比数列{an}中, ![]() ,a6+a7=3,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为 .
,a6+a7=3,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为 .
【答案】12
【解析】解:设正项等比数列{an}首项为a1 , 公比为q,
由题意可得 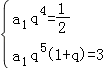 ,解之可得:a1=
,解之可得:a1= ![]() ,q=2,
,q=2,
故其通项公式为an= ![]() =2n﹣6 .
=2n﹣6 .
记Tn=a1+a2+…+an= ![]() =
= ![]() ,
,
Sn=a1a2…an=2﹣5×2﹣4…×2n﹣6=2﹣5﹣4+…+n﹣6= ![]() .
.
由题意可得Tn>Sn , 即 ![]() >
> ![]() ,
,
化简得:2n﹣1> ![]() ,即2n﹣
,即2n﹣ ![]() >1,
>1,
因此只须n> ![]() ,即n2﹣13n+10<0
,即n2﹣13n+10<0
解得 ![]() <n<
<n< ![]() ,
,
由于n为正整数,因此n最大为 ![]() 的整数部分,也就是12.
的整数部分,也就是12.
所以答案是:12
【考点精析】关于本题考查的解一元二次不等式和等差数列的前n项和公式,需要了解求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;前n项和公式:
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;前n项和公式:![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若a,b,c∈R,f(a),f(b),f(c)为某一个三角形的边长,则实数m的取值范围是( )
,若a,b,c∈R,f(a),f(b),f(c)为某一个三角形的边长,则实数m的取值范围是( )
A.[ ![]() ,1]
,1]
B.[0,1]
C.[1,2]
D.[ ![]() ,2]
,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校团委会组织某班以小组为单位利用周末时间进行一次社会实践活动,每个小组有5名同学,在活动结束后,学校团委会对该班的所有同学进行了测试,该班的A,B两个小组所有同学得分(百分制)的茎叶图如图所示,其中B组一同学的分数已被污损,但知道B组学生的平均分比A组同学的平均分高一分.
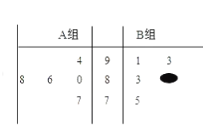
(1)若在B组学生中随机挑选1人,求其得分超过86分的概率;
(2)现从A、B两组学生中分别随机抽取1名同学,设其分数分别为m、n,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某一部件由四个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3或元件4正常工作,则部件正常工作.设四个电子元件的使用寿命(单位:小时)均服从正态分布![]() ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.
,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集为R,集合A={x|( ![]() )x≤1},B={x|x2﹣6x+8≤0},则A∩(RB)=( )
)x≤1},B={x|x2﹣6x+8≤0},则A∩(RB)=( )
A.{x|x≤0}
B.{x|2≤x≤4}
C.{x|0≤x<2或x>4}
D.{x|0<x≤2或x≥4}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com