
【题目】设![]() ,函数
,函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)求函数![]() 的极值;
的极值;
(3)若函数![]() 在区间
在区间![]() 上有唯一零点,试求
上有唯一零点,试求![]() 的值.
的值.
【答案】(1)![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ;(2)
;(2)![]() 有极大值
有极大值![]() ,无极小值;(3)
,无极小值;(3)![]() .
.
【解析】
(1)求出![]() ,解得
,解得![]() 或
或![]() ,则可探究当
,则可探究当![]() 时,当
时,当![]() 时,
时,![]() 的变化,从而求出单调区间;
的变化,从而求出单调区间;
(2)求出![]() ,令
,令![]() ,结合导数探究
,结合导数探究![]() 在
在![]() 的单调性,结合
的单调性,结合![]() ,可探究出
,可探究出![]() 随
随![]() 的变化情况,从而可求极值;
的变化情况,从而可求极值;
(3)令![]() ,可得
,可得![]() 在
在![]() 只有一个解,借助第二问可知
只有一个解,借助第二问可知![]() ,从而可求出
,从而可求出![]() 的值.
的值.
解:(1)当![]() 时,
时,![]() .易知
.易知![]() 的定义域为
的定义域为![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 递减;当
递减;当![]() 时,
时,![]() ,则
,则![]() 递增,
递增,
因此,![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() .
.
(2)![]() 的定义域为
的定义域为![]() ,则
,则![]() ,令
,令![]() ,
,
则![]() ,故
,故![]() 在
在![]() 单调递减,又知
单调递减,又知![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]()
因此![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
即当![]() 时,
时, ![]() 有极大值
有极大值![]() ,无极小值.
,无极小值.
(3)令![]() ,整理得:
,整理得:![]() 在
在![]() 只有一个解,
只有一个解,
即![]() 的图像与
的图像与![]() 的图像在
的图像在![]() 只有一个交点,由(2)知,
只有一个交点,由(2)知,
![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,且
单调递减,且![]() 有极大值
有极大值![]() ,
,
所以,![]() ,解得
,解得![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,且
是边长为2的正方形,且![]() ,若点E,F分别为AB和CD的中点.
,若点E,F分别为AB和CD的中点.
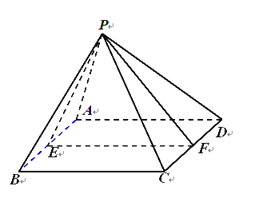
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人![]() 次数学考试的成绩,统计结果如下表:
次数学考试的成绩,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩(分) |
|
|
|
|
|
乙的成绩(分) |
|
|
|
|
|
(1)若从甲、乙两人中选出一人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若答对,则可参加复赛,否则被淘汰.
道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若至少答对其中
道,若至少答对其中![]() 道,则可参加复赛,否则被润汰.
道,则可参加复赛,否则被润汰.
已知学生甲、乙都只会![]() 道备选题中的
道备选题中的![]() 道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 至多只有一个公共点,求实数
至多只有一个公共点,求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() 的中点为
的中点为![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:对任意的
满足:对任意的![]() ,若
,若![]() ,则
,则![]() ,且
,且![]() ,设集合
,设集合![]() ,集合
,集合![]() 中元素最小值记为
中元素最小值记为![]() ,集合
,集合![]() 中元素最大值记为
中元素最大值记为![]() .
.
(1)对于数列:![]() ,写出集合
,写出集合![]() 及
及![]() ;
;
(2)求证:![]() 不可能为18;
不可能为18;
(3)求![]() 的最大值以及
的最大值以及![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,过点P(1,2)的直线l的参数方程为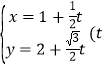 为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年末,武汉出现新型冠状病毒肺炎(![]() )疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为
)疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为![]() (
(![]() )且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为
)且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为![]() ,当
,当![]() 时,
时,![]() 最大,则
最大,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com