
【题目】已知曲线C的极坐标方程是ρ=1,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为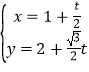 (t为参数).
(t为参数).
(1)写出直线l与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换![]() 得到曲线C′,设曲线C′上任一点为M(x,y),求x+2
得到曲线C′,设曲线C′上任一点为M(x,y),求x+2![]() y的最小值.
y的最小值.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】半径为1的圆O内切于正方形ABCD,正六边形EFGHPR内接于圆O,当EFGHPR绕圆心O旋转时,![]()
![]() 的取值范围是( )
的取值范围是( )
A.[1﹣![]() , 1+
, 1+![]() ]
]
B.[﹣1-![]() , ﹣1+
, ﹣1+![]() ]
]
C.[![]() ﹣
﹣![]() ,
, ![]() +
+![]() ]
]
D.[-![]() ﹣
﹣![]() , -
, -![]() +
+![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2![]() ,g(x)=1+
,g(x)=1+![]() sin 2x.
sin 2x.
(1)设x=x0是函数y=f(x)图象的一条对称轴,求g(x0)的值.
(2)若函数h(x)=f(x)+g(x)在区间![]() 上的最大值为2,求m的最小值.
上的最大值为2,求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是![]() ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是![]() .
.
(Ⅰ)若袋中共有10个球,
(i)求白球的个数;
(ii)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的数学期望Eξ.
(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于![]() . 并指出袋中哪种颜色的球个数最少.
. 并指出袋中哪种颜色的球个数最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cos θ.
(1)求出圆C的直角坐标方程;
(2)已知圆C与x轴相交于A,B两点,直线l:y=2x关于点M(0,m)(m≠0)对称的直线为l′.若直线l′上存在点P使得∠APB=90°,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,圆
轴的正半轴为极轴的极坐标系中,圆![]() 的方程为
的方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() 时,
时,![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x2﹣3x)ex
(1)求函数f(x)的单调递减区间;
(2)若方程(2x﹣3)ex= ![]() 有且仅有一个实根,求实数a的取值范围.
有且仅有一个实根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分13分)
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为![]() 元(
元(![]() 为常数,且
为常数,且![]() ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为![]() 元(
元(![]() ),根据市场调查,销售量
),根据市场调查,销售量![]() 与
与![]() 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
(Ⅰ)求该工厂的每日利润![]() 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价![]() 元的函数关系式;
元的函数关系式;
(Ⅱ)若![]() ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价![]() 为多少元时,该工厂的利润
为多少元时,该工厂的利润![]() 最大,并求最大值.
最大,并求最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设斜率为k(k>0)的直线l与椭圆C: ![]() +
+ ![]() =1交于A、B两点,且OA⊥OB.
=1交于A、B两点,且OA⊥OB. 
(Ⅰ)求直线l在y轴上的截距(用k表示);
(Ⅱ)求△AOB面积取最大值时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com