
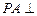 底面ABCD,底面为直角梯形,
底面ABCD,底面为直角梯形, ,
, 且AD=2,AB=BC=1,PA=
且AD=2,AB=BC=1,PA=
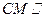 平面PAB;
平面PAB;

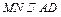 ,且
,且 ;
; ,且
,且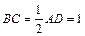 ,
,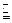 BC,即四边形BCMN为平行四边形,
BC,即四边形BCMN为平行四边形,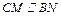 .
.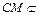 平面PAB,
平面PAB, 平面PAB,故
平面PAB,故 平面PAB. ……5分
平面PAB. ……5分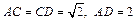 知
知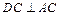 ,又
,又 ,所以
,所以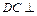 平面PAC,即平面P
平面PAC,即平面P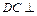 平面PAC,所以二面角D—PC—A的大小为90°. 于是二面角B—PC—A的大小为60°,过B作
平面PAC,所以二面角D—PC—A的大小为90°. 于是二面角B—PC—A的大小为60°,过B作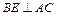 于E,过E作
于E,过E作 于F,连结BF,由三垂线定理知
于F,连结BF,由三垂线定理知 为二面角B—PC—A的平面角. ……9分
为二面角B—PC—A的平面角. ……9分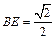 ,又易知△PBC为Rt△,且
,又易知△PBC为Rt△,且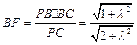 ,
, ,解得
,解得 ……11分
……11分 ……12分
……12分 |
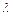 ). ……2分
). ……2分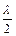 ),所以
),所以 .
. ,而
,而 ,即
,即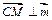 .
.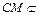 平面PAB,所以
平面PAB,所以 平面PAB. ……6分
平面PAB. ……6分 (Ⅱ)设平面PBC的法向量为
(Ⅱ)设平面PBC的法向量为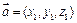 .
.  ∴
∴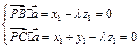
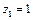 ,则
,则 ,∴
,∴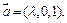
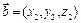 .
.  ∴
∴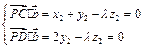
 ,则
,则 ∴
∴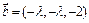 . ……9分
. ……9分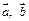 的方向可知
的方向可知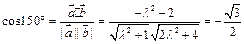 ,解得
,解得 . ……11分
. ……11分 . ……12分
. ……12分

科目:高中数学 来源:不详 题型:解答题
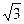 。AD=
。AD=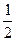 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 BCD与直角梯形ADEF所
BCD与直角梯形ADEF所 垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2。
垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com