
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F,G,H分别为AA1 , AB,BB1 , B1C1的中点,则异面直线EF与GH所成的角等于( ) 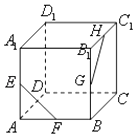
A.45°
B.60°
C.90°
D.120°
科目:高中数学 来源: 题型:
【题目】欧阳修《卖油翁)中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌漓沥之,自钱孔入,而钱不湿”,可见“行行出状元”,卖油翁的技艺让人叹为观止,若铜钱是直径为4 cm的圆,中间有边长为l cm的正方形孔.若随机向铜钱上滴一滴油(设油滴整体落在铜钱上).则油滴(设油滴是直径为0.2 cm的球)正好落入孔中(油滴整体落入孔中)的概率是_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.
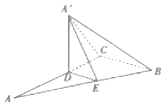
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足a1=2,Sn-4Sn-1-2=0(n≥2,n∈Z).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=log2an,Tn为{bn}的前n项和,求证![]() <2.
<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)<0且f(﹣1)=0则不等式f(x)g(x)<0的解集为( )
A.(﹣1,0)∪(1,+∞)
B.(﹣1,0)∪(0,1)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣∞,﹣1)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市A,B两所中学的学生组队参加辩论赛,A中学推荐了3名男生、2名女生,B中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队.
(1)求A中学至少有1名学生入选代表队的概率;
(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象如图所示,将f(x)的图象向左平移
)的部分图象如图所示,将f(x)的图象向左平移 ![]() 个单位后的解析式为( )
个单位后的解析式为( ) 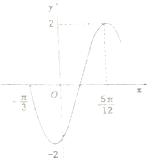
A.y=2sin(2x﹣ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin(2x)
D.y=2sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在BC,AD上,EF∥AB.现将四边形ABCD沿EF折起,使平面ABEF⊥平面EFDC.
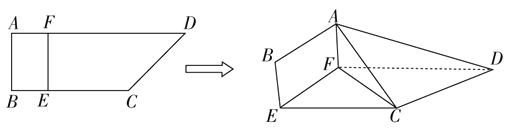
(Ⅰ)若BE=1,是否在折叠后的线段AD上存在一点P,且![]() ,使CP∥平面ABEF?若存在,求出λ的值,若不存在,说明理由;
,使CP∥平面ABEF?若存在,求出λ的值,若不存在,说明理由;
(Ⅱ)求三棱锥A-CDF的体积的最大值,并求出此时二面角E-AC-F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 
(1)当x≤0时,解不等式f(x)≥﹣1;
(2)写出该函数的单调区间;
(3)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com