
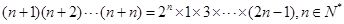 ”时,从“
”时,从“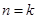 ”变到 “
”变到 “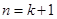 ”时,左边应增乘的因式是
”时,左边应增乘的因式是 A.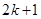 | B.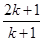 | C. | D.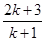 |
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
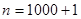 时它也成立,下列判断中,正确的是( )
时它也成立,下列判断中,正确的是( )| A.P(k)对k=2013成立 | B.P(k)对每一个自然数k成立 |
| C.P(k)对每一个正偶数k成立 | D.P(k)对某些偶数可能不成立 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
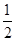 +
+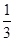 +…+
+…+ <n(n∈N*,n>1)时,在证明过程的第二步从n=k到n=k+1时,左边增加的项数是 ( )
<n(n∈N*,n>1)时,在证明过程的第二步从n=k到n=k+1时,左边增加的项数是 ( )| A.2k | B.2k-1 | C.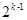 | D.2k+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com