
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)过点![]() 的直线
的直线![]() 与平行四边形
与平行四边形![]() 围成的区域(包括边界)有公共点,求直线
围成的区域(包括边界)有公共点,求直线![]() 的倾斜角
的倾斜角![]() 的取值范围;
的取值范围;
(3)对角线![]() 所在的直线与圆
所在的直线与圆![]() :
:![]() 没有交点,求实数
没有交点,求实数![]() 的取值范围.
的取值范围.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】定义:曲线![]() 称为椭圆
称为椭圆![]() 的“倒椭圆”.已知椭圆
的“倒椭圆”.已知椭圆![]() ,它的“倒椭圆”
,它的“倒椭圆”![]() .
.
(1)写出“倒椭圆”![]() 的一条对称轴、一个对称中心;并写出其上动点横坐标x的取值范围.
的一条对称轴、一个对称中心;并写出其上动点横坐标x的取值范围.
(2)过“倒椭圆”![]() 上的点P,作直线PA垂直于x轴且垂足为点A,作直线PB垂直于y轴且垂足为点B,求证:直线AB与椭圆
上的点P,作直线PA垂直于x轴且垂足为点A,作直线PB垂直于y轴且垂足为点B,求证:直线AB与椭圆![]() 只有一个公共点.
只有一个公共点.
(3)是否存在直线l与椭圆![]() 无公共点,且与“倒椭圆”
无公共点,且与“倒椭圆”![]() 无公共点?若存在,请给出满足条件的直线l,并说明理由;若不存在,请说明理由.
无公共点?若存在,请给出满足条件的直线l,并说明理由;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
分类 | 积极参加 班级工作 | 不太主动参 加班级工作 | 总计 |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
总计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABC,则二面角D﹣AF﹣B的平面角余弦值的取值范围是_____.
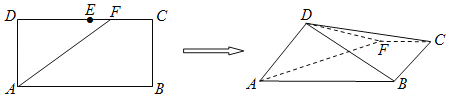
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为F1,F2,离心率为
的左、右焦点为F1,F2,离心率为![]() ,且点
,且点![]() 在椭圆上.
在椭圆上.
(1)求椭圆C的标准方程;
(2)若直线l过点M(0,﹣2)且与椭圆C相交于A,B两点,且△OAB(O为坐标原点)的面积为![]() ,求出直线l的方程.
,求出直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABED中,AB//DE,AB![]() BE,点C在AB上,且AB
BE,点C在AB上,且AB![]() CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE
CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE![]() .
.
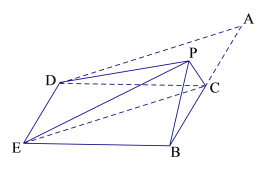
(1)求证:平面PBC ![]() 平面DEBC;
平面DEBC;
(2)求三棱锥P-EBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人造地球卫星绕地球运行遵循开普勒行星运动定律:如图,卫星在以地球的中心为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星与地心的连线)在相同的时间内扫过的面积相等设该椭圆的长轴长、焦距分别为![]() ,
,![]() .某同学根据所学知识,得到下列结论:
.某同学根据所学知识,得到下列结论:

①卫星向径的取值范围是![]()
②卫星向径的最小值与最大值的比值越大,椭圆轨道越扁
③卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间
④卫星运行速度在近地点时最小,在远地点时最大
其中正确的结论是( )
A.①②B.①③C.②④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com