
【题目】甲、乙两人同时参加一个外贸公司的招聘,招聘分笔试与面试两部分,先笔试后面试.甲笔试与面试通过的概率分别为0.8,0.5,乙笔试与面试通过的概率分别为0.8,0.4,且笔试通过了才能进入面试,面试通过则直接招聘录用,两人笔试与面试相互独立互不影响.
(1)求这两人至少有一人通过笔试的概率;
(2)求这两人笔试都通过却都未被录用的概率;
(3)记这两人中最终被录用的人数为X,求X的分布列和数学期望.
【答案】(1)0.96;(2)0.192;(3)分布列见解析,数学期望0.72
【解析】
(1)利用独立事件与对立事件的概率公式求解即可;(2)直接利用独立事件的概率公式求解即可;(3)X可取0,1,2, 利用独立事件与对立事件的概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得![]() 的数学期望.
的数学期望.
(1)设“这两人至少有一人通过笔试”为事件A,
则P(A)=1![]() P(
P(![]() )=1
)=1![]() (1
(1![]() 0.8)2=0.96.
0.8)2=0.96.
(2)设“这两人笔试都通过却都未被录用”为事件B,
则P(B)=0.82×(1![]() 0.5)×(1
0.5)×(1![]() 0.4)=0.192.
0.4)=0.192.
(3)甲、乙两人被录用的概率分别为0.8×0.5=0.4,0.8×0.4=0.32.
由题意可得X可取0,1,2,则
P(X=0)=(1![]() 0.4)×(1
0.4)×(1![]() 0.32)=0.408,
0.32)=0.408,
P(X=1)=(1![]() 0.4)×0.32+0.4×(1
0.4)×0.32+0.4×(1![]() 0.32)=0.464,
0.32)=0.464,
P(X=2)=0.4×0.32=0.128,
所以X的分布列为
X | 0 | 1 | 2 |
P | 0.408 | 0.464 | 0.128 |
故E(X)=0×0.408+1×0.464+2×0.128=0.72.


科目:高中数学 来源: 题型:
【题目】现有10名教师,其中男教师6名,女教师4名.
(1)现要从中选2名去参加会议,有多少种不同的选法?
(2)选出2名男教师或2名女教师去外地学习的选法有多少种?
(3)现要从中选出男、女老师各2名去参加会议,有多少种不同的选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,实轴长为6,渐近线方程为
,实轴长为6,渐近线方程为![]() ,动点
,动点![]() 在双曲线左支上,点
在双曲线左支上,点![]() 为圆
为圆![]() 上一点,则
上一点,则![]() 的最小值为
的最小值为
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥中![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的中点,直线
上的中点,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,点
,点![]() 在
在![]() 上移动.
上移动.
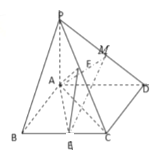
(Ⅰ)证明:无论点![]() 在
在![]() 上如何移动,都有平面
上如何移动,都有平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 恰为
恰为![]() 的中点时,二面角
的中点时,二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋里装有大小相同的5个小球,其中红色两个,其余3个颜色各不相同![]() 现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是______;若变量X为取出的三个小球中红球的个数,则X的数学期望
现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是______;若变量X为取出的三个小球中红球的个数,则X的数学期望![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱(已知:![]() 则认为
则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般,
线性相关性一般,![]() ,则认为y与x线性相关性较弱)
,则认为y与x线性相关性较弱)
(2)求y与x的线性回归方程,并预测该地区2019年足球特色学校的个数(精确到个位)
参考公式:
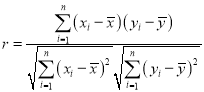
![]() ;
;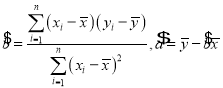
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程,并求其离心率;
的方程,并求其离心率;
(2)过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,设点
,设点![]() 为第四象限内一点且在椭圆
为第四象限内一点且在椭圆![]() 上(点
上(点![]() 不在直线
不在直线![]() 上),点
上),点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,直线
,直线![]() 与
与![]() 交于另一点
交于另一点![]() .设
.设![]() 为原点,判断直线
为原点,判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com