设f(x)是定义在[-1,1]上的偶函数,当x∈[-1,0]时,f(x)=-2ax+4x3.
(Ⅰ) 若f(x)在(0,1]上为增函数,求a的取值范围;
(Ⅱ) 是否存在正整数a,使f(x)的图象的最高点落在直线y=12上?若存在,求出a的值;若不存在,请说明理由.
解:因为当x∈[-1,0]时,f(x)=-2ax+4x
3.
所以当x∈(0,1]时,f(x)=f(-x)=2ax-4x
3,
∴
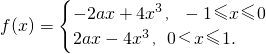
(Ⅰ)由题设f(x)在(0,1]上为增函数,∴f'(x)≥0在x∈(0,1]恒成立,
即2a-12x
2≥0对x∈(0,1]恒成立,于是,a≥6x
2,从而a≥(6x
2)
max=6.
即a的取值范围是[6,+∞)
(Ⅱ)因f(x)为偶函数,故只需研究函数f(x)=2ax-4x
3在x∈(0,1]的最大值.
令f'(x)=2a-12x
2=0,得

.…(8分)
若
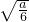
∈(0,1],即0<a≤6,则
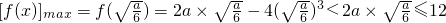
,
故此时不存在符合题意的a;
若
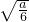
>1,即a>6,则f(x)在(0,1]上为增函数,于是[f(x)]
max=f(1)=2a-4.
令2a-4=12,故a=8.综上,存在a=8满足题设.…(12分)
分析:(Ⅰ)先求出函数在(0,1]上的解析式,再利用f'(x)≥0在x∈(0,1]恒成立可求;(Ⅱ)存在,令f'(x)>0,即可求出a的取值范围,便可知0<a≤6不符合题意,当a>6时[f(x)]
max=f(1)=2a-4-12,即可求出满足题意的a的值.
点评:本题通过函数的知识来切入到导数,考查了利用导数求函数的单调性以及闭区间的最值问题,考查了学生的逻辑思维能力与推理能力,函数及导数的应用是数学的难点,也是高考的热点,属于中档题.

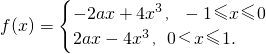
 .…(8分)
.…(8分)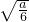 ∈(0,1],即0<a≤6,则
∈(0,1],即0<a≤6,则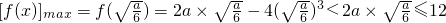 ,
,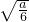 >1,即a>6,则f(x)在(0,1]上为增函数,于是[f(x)]max=f(1)=2a-4.
>1,即a>6,则f(x)在(0,1]上为增函数,于是[f(x)]max=f(1)=2a-4.
