
【题目】如图,在直三棱柱 ![]() 中,平面
中,平面 ![]() 侧面
侧面 ![]() ,且
,且 ![]() .
. 
(1)求证: ![]() ;
;
(2)若直线 ![]() 与平面
与平面 ![]() 所成角的大小为
所成角的大小为 ![]() ,求锐二面角
,求锐二面角 ![]() 的大小.
的大小.
【答案】
(1)如图,取 ![]() 的中点D,连接AD,
的中点D,连接AD,
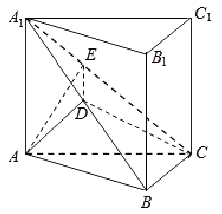
因为 ![]() ,所以
,所以 ![]() ,
,
由平面 ![]() ⊥侧面
⊥侧面 ![]() ,且平面
,且平面 ![]() ,
,
得AD⊥平面 ![]() ,
,
又BC ![]() 平面
平面 ![]() ,所以AD⊥BC,
,所以AD⊥BC,
因为三棱柱 ![]() 是直三棱柱,则
是直三棱柱,则 ![]() ⊥底面ABC,
⊥底面ABC,
所以 ![]()
又 ![]() ,从而BC⊥侧面
,从而BC⊥侧面 ![]() ,又AB
,又AB ![]() 侧面
侧面 ![]() ,
,
故AB⊥BC.
(2)连接CD,由(1)可知AD⊥平面 ![]() ,则CD是AC在平面
,则CD是AC在平面 ![]() 内的射影,
内的射影,
∴∠ACD即为直线AC与平面 ![]() 所成的角,则∠ACD=30°.
所成的角,则∠ACD=30°.
在等腰直角 ![]() 中,
中, ![]() ,且点D是
,且点D是 ![]() 的中点,
的中点,
∴ ![]() ,又
,又 ![]() ,∠ACD=30°,∴AC=
,∠ACD=30°,∴AC= ![]() .
.
过点A作AE⊥ ![]() 于点E,连接DE,由(1)知AD⊥平面
于点E,连接DE,由(1)知AD⊥平面 ![]() ,则
,则 ![]() ,又
,又 ![]() ,
,
∴ ![]() ,
,
∴∠AED即为二面角 ![]() 的一个平面角.
的一个平面角.
在直角△ ![]() 中,
中, ![]() ,
,
又 ![]() ,
,
∴ ![]() ,
,
又二面角 ![]() 为锐二面角,∴∠AED=60°,
为锐二面角,∴∠AED=60°,
即二面角 ![]() 的大小为60°.
的大小为60°.

【解析】本小题主要考查线线垂直,线面垂直,二面角等基础知识,考查推理论证能力、运算求解能力、空间想象能力,并考查应用向量知识解决立体几何问题的能力.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则 ①OE⊥BD1;
②OE∥面A1C1D;
③三棱锥A1﹣BDE的体积为定值;
④OE与A1C1所成的最大角为90°.
上述命题中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x在区间[2,3]上单调递增,则实数a的取值范围是( )
A.[﹣2,+∞)
B.[﹣3,+∞)
C.[0,+∞)
D.(﹣∞,﹣2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=plnx+(p﹣1)x2+1.
(1)讨论函数f(x)的单调性;
(2)当P=1时,f(x)≤kx恒成立,求实数k的取值范围;
(3)证明:1n(n+1)<1+ ![]() …+
…+ ![]() (n∈N+).
(n∈N+).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十三届全运会将在2017年8月在天津举行,组委会在2017年1月对参加接待服务的10名宾馆经理进行为期半月的培训,培训结束,组织了一次培训结业测试,10人考试成绩如下(满分为100分):
75 84 65 90 88 95 78 85 98 82
(1)以成绩的十位为茎个位为叶作出本次结业成绩的茎叶图,并计算平均成绩与成绩中位数 ;
(2)从本次结业成绩在80分以上的人员中选3人,这3人中成绩在90分(含90分)以上的人数为 ![]() ,求
,求 ![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点. 
(1)证明:B1C1⊥平面BDE;
(2)求二面角D﹣BE﹣C1的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域均为D的三个函数f(x),g(x),h(x)满足条件:对任意x∈D,点(x,g(x)与点(x,h(x)都关于点(x,f(x)对称,则称h(x)是g(x)关于f(x)的“对称函数”.已知g(x)= ![]() ,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是
,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com