
【题目】已知等差数列![]() 的首项为p,公差为
的首项为p,公差为![]() ,对于不同的自然数
,对于不同的自然数![]() ,直线
,直线![]() 与
与![]() 轴和指数函数
轴和指数函数![]() 的图象分别交于点
的图象分别交于点![]() 与
与![]() (如图所示),记
(如图所示),记![]() 的坐标为
的坐标为![]() ,直角梯形
,直角梯形![]() 、
、![]() 的面积分别为
的面积分别为![]() 和
和![]() ,一般地记直角梯形
,一般地记直角梯形![]() 的面积为
的面积为![]() .
.

(1)求证:数列![]() 是公比绝对值小于1的等比数列;
是公比绝对值小于1的等比数列;
(2)设![]() 的公差
的公差![]() ,是否存在这样的正整数
,是否存在这样的正整数![]() ,构成以
,构成以![]() ,
,![]() ,
,![]() 为边长的三角形?并请说明理由;
为边长的三角形?并请说明理由;
(3)设![]() 的公差
的公差![]() 为已知常数,是否存在这样的实数p使得(1)中无穷等比数列
为已知常数,是否存在这样的实数p使得(1)中无穷等比数列![]() 各项的和
各项的和![]() ?并请说明理由.
?并请说明理由.
【答案】(1)证明见解析(2)不存在,详见解析(3)存在,证明见解析
【解析】
(1)![]() ,直角梯形
,直角梯形![]() 的两底长度
的两底长度![]() ,
,![]() .高为
.高为![]() ,利用梯形面积公式表示出
,利用梯形面积公式表示出![]() .利用等比数列定义进行证明即可;
.利用等比数列定义进行证明即可;
(2)![]() ,
, ,以
,以![]() ,
,![]() ,
,![]() 为边长能构成一个三角形,则
为边长能构成一个三角形,则![]() 考查不等式解的情况作解答;
考查不等式解的情况作解答;
(3)利用无穷等比数列求和公式,将![]() 化简为
化简为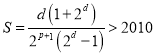 ,则
,则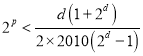 ,探讨p的存在性.
,探讨p的存在性.
解:(1)![]() ,
,![]() ,
,
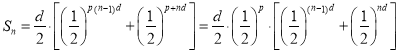 ,
,
对于任意自然数n,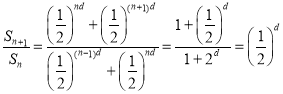 ,
,
所以数列![]() 是等比数列且公比
是等比数列且公比![]() ,
,
因为![]() ,所以
,所以![]() ;
;
(2)![]() ,
, ,
,
对每个正整数![]() ,
,![]() ,
,
若以![]() ,
,![]() ,
,![]() 为边长能构成一个三角形,
为边长能构成一个三角形,
则![]() ,即
,即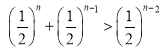 ,
,
即有![]() ,这是不可能的.
,这是不可能的.
所以对每一个正整数![]() ,以
,以![]() ,
,![]() ,
,![]() 为边长不能构成三角形;
为边长不能构成三角形;
(3)由(1)知,![]() ,
,![]() ,
,
所以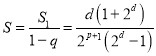 ,
,
若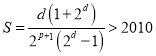 ,则
,则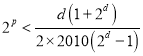
两边取对数,知只要![]() 取值为小于
取值为小于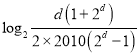 的实数,
的实数,
就有![]() .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形,一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.分形几何学不仅让人们感悟到科学与艺木的融合,数学与艺术审美的统一,而且还有其深刻的科学方法论意义.如图,由波兰数学家谢尔宾斯基1915年提出的谢尔宾斯基三角形就属于-种分形,具体作法是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形.

若在图④中随机选取-点,则此点取自阴影部分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且函数
,且函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
(1)若存在![]() ,使等式
,使等式![]() 成立,求实数m的最大值和最小值
成立,求实数m的最大值和最小值
(2)若当![]() 时不等式
时不等式![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的定义域为
的定义域为![]() 恰是不等式
恰是不等式![]() 的解集,其值域为
的解集,其值域为![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .
.
(1)求函数![]() 定义域为
定义域为![]() 和值域
和值域![]() ;
;
(2)是否存在负实数![]() ,使得
,使得![]() 成立?若存在,求负实数
成立?若存在,求负实数![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(3)若函数![]() 在定义域
在定义域![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 的左右两个焦点,过
的左右两个焦点,过![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在第一象限),
在第一象限),![]() 的周长为8,
的周长为8,![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() ,
,![]() 为
为![]() 的左右顶点,直线
的左右顶点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在一条景观道的一端有一个半径为![]() 米的圆形摩天轮O,逆时针
米的圆形摩天轮O,逆时针![]() 分钟转一圈,从
分钟转一圈,从![]() 处进入摩天轮的座舱,
处进入摩天轮的座舱,![]() 垂直于地面
垂直于地面![]() ,在距离
,在距离![]() 处
处![]() 米处设置了一个望远镜
米处设置了一个望远镜![]() .
.

(1)同学甲打算独自乘坐摩天轮,但是其母亲不放心,于是约定在登上摩天轮座舱![]() 分钟后,在座舱内向其母亲挥手致意,而其母亲则在望远镜
分钟后,在座舱内向其母亲挥手致意,而其母亲则在望远镜![]() 中仔细观看.问望远镜
中仔细观看.问望远镜![]() 的仰角
的仰角![]() 应调整为多少度?(精确到1度)
应调整为多少度?(精确到1度)
(2)在同学甲向其母亲挥手致意的同时,同一座舱的另一名乘客乙在拍摄地面上的一条绿化带![]() ,发现取景的视角
,发现取景的视角![]() 恰为
恰为![]() ,求绿化带
,求绿化带![]() 的长度(精确到1米)
的长度(精确到1米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,规定90分及以上为合格:
,规定90分及以上为合格:
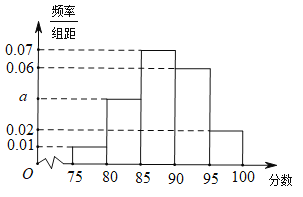
(1)求图中a的值;
(2)根据频率分布直方图估计该地区学员交通法规考试合格的概率;
(3)若三个人参加交通法规考试,估计这三个人至少有两人合格的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线系![]() (
(![]() ),则下列命题中是真命题的个数是( )
),则下列命题中是真命题的个数是( )
①存在一个圆与所有直线相交;
②存在一个圆与所有直线不相交;
③存在一个圆与所有直线相切;
④![]() 中所有直线均经过一个定点;
中所有直线均经过一个定点;
⑤不存在定点![]() 不在
不在![]() 中的任一条直线上;
中的任一条直线上;
⑥对于任意整数![]() ,存在正
,存在正![]() 边形,其所有边均在
边形,其所有边均在![]() 中的直线上;
中的直线上;
⑦![]() 中的直线所能围成的正三角形面积都相等.
中的直线所能围成的正三角形面积都相等.
A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)在函数![]() 的图象上取
的图象上取![]() 两个不同的点,令直线AB的斜率
两个不同的点,令直线AB的斜率
为k,则在函数的图象上是否存在点![]() ,且
,且![]() ,使得
,使得![]() ?若存
?若存
在,求A,B两点的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com