分析:法一:(Ⅰ)先证明直线AB
1垂直平面A
1BD内的两条相交直线BD、A
1B,即可证明AB
1⊥平面A
1BD;
(Ⅱ)设AB
1与A
1B交于点C,在平面A
1BD中,作GF⊥A
1D于F,连接AF,
说明∠AFG为二面A-A
1B-B的平面角,然后求二面角A-A
1D-B的大小.
法二:取BC中点O,连接AO,以0为原点,
,,的方向为x、y、z轴的正方向建立空间直角坐标系,求出
•=0,•=0,
即可证明AB
1⊥平面A
1BD.
求出平面A
1AD的法向量为
=(x,y,z),
为平面A
1BD的法向量,
然后求二者的数量积,求二面角A-A
1D-B的大小.
解答: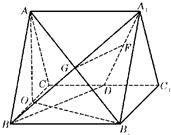
解:法一:(Ⅰ)取BC中点O,连接AO、
∵△ABC为正三角形,∴AO⊥BC.
∵正三棱柱ABC-A
1B
1C
1中,平面ABC⊥平面BCC
1B
1,
∴AO⊥平面BCC
1B
1,
连接B
1O,在正方形BB
1C
1C中,O、D分别为BC、CC
1的中点,
∴B
1O⊥BD,
∴AB
1⊥BD.
在正方形ABB
1A
1中,AB
1⊥A
1B,
∴AB
1⊥平面A
1BD.
(Ⅱ)设AB
1与A
1B交于点G,在平面A
1BD中,作GF⊥A
1D于F,连接AF,由(Ⅰ)得AB
1⊥平面A
1BD,
∴∠AFG为二面A-A
1D-B的平面角,
在△AA
1D中,由等面积法可求得AF=
,
又∵AG=
AB1=
,
∴sin∠AFG=
==,
所以二面角A-A
1D-B的大小为arcsin
.

法二:(Ⅰ)取BC中点O,连接AO.
∵△ABC为正三角形,∴AO⊥BC、
∵正三棱柱ABC-A
1B
1C
1中,平面ABC⊥平面BCC
1B
1,
∴AO⊥平面BCC
1B
1,
取B
1C
1中点O
1,以0为原点,
,,的方向为x、y、z轴的正方向建立空间直角坐标系,则B(1,0,0),D(-1,1,0),A
1(0,2,
),A(0,0,
),B
1(1,2,0),
∴
=(1,2,-),=(-2,1,0),=(-1,2,)∵
•=-2+2+0=0,•=-1+4-3=0,
∴
⊥
,⊥
,
∴AB
1⊥平面A
1BD.
(Ⅱ)设平面A
1AD的法向量为
=(x,y,z),
=(-1,1,-),=(0,2,0).
∵
⊥
,⊥
,
∴
∵
∴
令z=1得
=(-
,0,1)为平面A
1AD的一个法向量.
由(Ⅰ)知AB
1⊥A
1BD.
∴
为平面A
1BD的法向量.
cos<
,
>=
=
=-
.
∴二面角A-A
1D-B的大小为arccos
.
点评:本题考查直线与平面垂直的判定,二面角的求法,考查空间想象能力,逻辑思维能力,计算能力,是中档题.

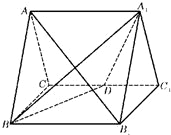 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 解:法一:(Ⅰ)取BC中点O,连接AO、
解:法一:(Ⅰ)取BC中点O,连接AO、 法二:(Ⅰ)取BC中点O,连接AO.
法二:(Ⅰ)取BC中点O,连接AO.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.