【题目】设命题p：实数x满足 
＜0，其中a＞0，命题q：实数x满足 
．
（1）若a=1，且p∧q为真，求实数x的取值范围；
（2）若￢p是￢q的充分不必要条件，求实数a的取值范围．
【答案】
（1）解：命题p：a=1时，由 
＜0，化为：（x﹣1）（x﹣3）＜0，解得1＜x＜3．
命题q：实数x满足 
，
化为： 
，解得 
，解得2＜x＜3．
∵p∧q为真，∴ 
，解得2＜x＜3．
∴实数x的取值范围是（2，3）
（2）解：由（1）可得：命题q：实数x满足：2＜x＜3．
命题p：实数x满足 
＜0，其中a＞0，化为（x﹣a）（x﹣3a）＜0，解得a＜x＜3a．
∵￢p是￢q的充分不必要条件，
∴q是p的充分不必要条件，
∴ 
，且等号不能同时成立，解得1≤a≤2．
∴实数a的取值范围是[1，2]
【解析】（1）命题p：a=1时，由 ＜0，化为：（x﹣1）（x﹣3）＜0，解出即可得出．命题q：实数x满足 
，化为： 
，解得x范围．由p∧q为真，可得命题p与q都为真命题．（2）由（1）可得：命题q：实数x满足：2＜x＜3．命题p：实数x满足 ＜0，其中a＞0，化为（x﹣a）（x﹣3a）＜0，解得x范围．由￢p是￢q的充分不必要条件，可得q是p的充分不必要条件，即可得出．
【考点精析】解答此题的关键在于理解复合命题的真假的相关知识，掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反；“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；“p或q”形式复合命题当p与q同为假时为假，其他情况时为真．
科目：高中数学 来源： 题型：
【题目】某中学拟在高一下学期开设游泳选修课，为了了解高一学生喜欢游泳是否与性别有关，现从高一学生中抽取
人做调查，得到如下
列联表：
已知在这
人中随机抽取一人抽到喜欢游泳的学生的概率为
，
（Ⅰ）请将上述列联表补充完整，并判断是否有
％的把握认为喜欢游泳与性别有关？并说明你的理由；
（Ⅱ）针对问卷调查的
名学生，学校决定从喜欢游泳的人中按分层抽样的方法随机抽取
人成立游泳科普知识宣传组，并在这
人中任选两人作为宣传组的组长，求这两人中至少有一名女生的概率，参考公式： 
,其中
.参考数据：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，圆锥曲线C的极坐标方程为ρ2= 
，F1是圆锥曲线C的左焦点．直线l： 
（t为参数）．
（1）求圆锥曲线C的直角坐标方程和直线l的直角坐标方程；
（2）若直线l与圆锥曲线C交于M，N两点，求|F1M|+|F1N|．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】圆心在直线2x－3y－1＝0上的圆与x轴交于A(1,0)，B(3,0)两点，则圆的方程为( )
A.(x－2)2＋(y＋1)2＝2
B.(x＋2)2＋(y－1)2＝2
C.(x－1)2＋(y－2)2＝2
D.(x－2)2＋(y－1)2＝2
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2﹣lnx．
（1）求函数y=f（x）的单调区间；
（2）设g（x）=x﹣t，若函数h（x）=g（x）﹣f（x）在[ 
，e]上（这里e≈2.718）恰有两个不同的零点，求实数t的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）若
，求曲线
在点
处的切线；
（2）若函数
在其定义域内为增函数，求正实数
的取值范围；
（3）设函数
，若在
上至少存在一点
，使得
成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
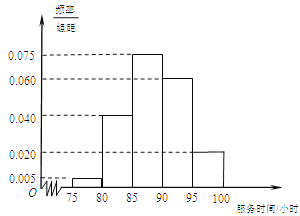
【题目】某市规定，高中学生三年在校期间参加不少于
小时的社区服务才合格．教育部门在全市随机抽取200位学生参加社区服务的数据，按时间段
，
，
，
，
（单位：小时）进行统计，其频率分布直方图如图所示．
（Ⅰ）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计
从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；
（Ⅱ）从全市高中学生（人数很多）中任意选取3位学生，记
为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量
的分布列和数学期望
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】斜三棱柱ABC﹣A1B1C1中，AA1=AC=BC=2，∠A1AC=∠C1CB=60°，且平面ACC1A1⊥平面BCC1B1 ， 则A1B的长度为 ．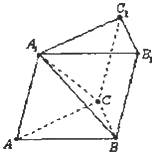 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
