
分析 (1)根据指数函数以及二次函数的性质求出p为真时的m的范围即可;
(2)根据二次函数的性质,求出m的范围,从而求出复合命题的m的范围.
解答 解:(1)p为真命题:
∵函数$f(x)={2^{{x^2}-2x}}-m$在R上有零点,
∴$f(x)={2^{{x^2}-2x}}-m=0$有解,
∴${2^{{x^2}-2x}}=m$有解,
∴m=${2}^{{(x-1)}^{2}-1}$≥2-1=$\frac{1}{2}$,
∴m≥$\frac{1}{2}$;
(2)函数f(x)=x2+2mx+n在[1,2]上单调递增,
对称轴x=-m,
∴-m≤1,.
∴m≥-1,
∵p∧q,所以p,q均为真,
所以$m≥\frac{1}{2}$.
点评 本题考查了复合命题的判断,考查二次函数的性质,是一道基础题.


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 4030 | D. | 4031 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
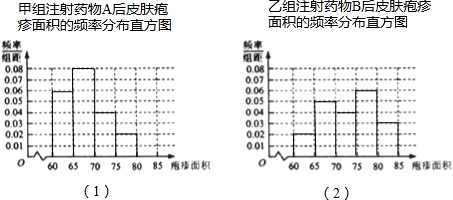
| 疱疹面积小于70mm2 | 疱疹面积不小于70mm2 | 合计 | |
| 注射药物A | |||
| 注射药物B | |||
| 合计 |
| P(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com