
分析 (Ⅰ)由x=ρcosθ,y=ρsinθ,可得A,B的直角坐标,求得AB的斜率,由点斜式方程可得直线方程;
(Ⅱ)运用点到直线的距离公式,结合三角函数的辅助角公式,由正弦函数的值域,即可得到所求最大值.
解答 解:(Ⅰ) 将A、B化为直角坐标为A(2cosπ,2sinπ)、$B(2cos\frac{4π}{3},2sin\frac{4π}{3})$,
即A、B的直角坐标分别为A(-2,0)、$B(-1,-\sqrt{3})$,
即有${k_{AB}}=\frac{{-\sqrt{3}-0}}{-1+2}=-\sqrt{3}$,
可得直线AB的方程为$y-0=-\sqrt{3}(x+2)$,
即为$\sqrt{3}x+y+2\sqrt{3}=0$.
(Ⅱ)设M(2cosθ,sinθ),
它到直线AB距离$d=\frac{{|2\sqrt{3}cosθ+sinθ+2\sqrt{3}|}}{2}$
=$\frac{{|\sqrt{13}sin(θ+φ)+2\sqrt{3}|}}{2}$,(其中$tanφ=2\sqrt{3}$)
当sin(θ+φ)=1时,d取得最大值,
可得${d_{max}}=\frac{{\sqrt{13}+2\sqrt{3}}}{2}$.
点评 本题考查直角坐标和极坐标的互化,直线方程的求法和运用,同时考查三角函数的辅助角公式和正弦函数的值域的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
根据统计资料,某工艺品厂的日产量最多不超过20件根据统计资料,每日产品废品率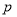 与日产量
与日产量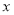 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率=
(日产品废品率= ×100%) .已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
×100%) .已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润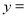 日正品赢利额
日正品赢利额 日废品亏损额)
日废品亏损额)
(1)将该车间日利润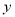 (千元)表示为日产量
(千元)表示为日产量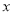 (件)的函数;
(件)的函数;
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.
如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{4}$,-$\frac{3}{5}$)∪($\frac{3}{5}$,$\frac{3}{4}$] | B. | [-1,-$\frac{3}{4}$)∪($\frac{3}{4}$,1] | C. | ($\frac{3}{5}$,$\frac{3}{4}$] | D. | [-$\frac{3}{4}$,-$\frac{3}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
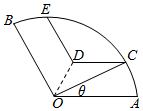
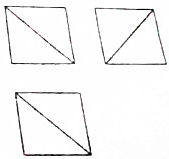 如图,粗线画出的是一个正方体被两个平行平面所截后的几何体的三视图,图中三个正方形的边长为4,则此几何体的表面积为( )
如图,粗线画出的是一个正方体被两个平行平面所截后的几何体的三视图,图中三个正方形的边长为4,则此几何体的表面积为( )| A. | 40+8$\sqrt{3}$ | B. | 48+8$\sqrt{3}$ | C. | 40+16$\sqrt{3}$ | D. | 48+16$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
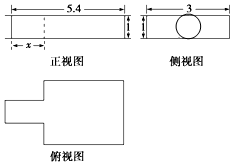 中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为( )| A. | 1.2 | B. | 1.6 | C. | 1.8 | D. | 2.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com