
【题目】已知函数![]() (
(![]() ).
).
(Ⅰ)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() 有两个极值点,求实数a的取值范围;
有两个极值点,求实数a的取值范围;
(Ⅲ)若![]() ,求
,求![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
由题意得![]() ;
;
(Ⅰ)当![]() 时,求得
时,求得![]() ,
,![]() ,根据点斜式方程即可求出切线方程;
,根据点斜式方程即可求出切线方程;
(Ⅱ)由题意得![]() 两个不等的正根,令
两个不等的正根,令![]() ,则
,则![]() ,由此可得函数
,由此可得函数![]() 的单调性,由此可求出答案;
的单调性,由此可求出答案;
(Ⅲ)由题意可得![]() ,由二阶导的取值符号可得到
,由二阶导的取值符号可得到![]() 的单调性,得到
的单调性,得到![]() ,由此可求出函数
,由此可求出函数![]() 在
在![]() 上单调递减,从而求出最值.
上单调递减,从而求出最值.
解:∵![]() ,
,
∴![]() ;
;
(Ⅰ)当![]() 时,
时,![]() ,
,![]() ,
,
∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() ;
;
(Ⅱ)∵若![]() 有两个极值点,
有两个极值点,
∴![]() 有两个不等的正根,即
有两个不等的正根,即![]() 两个不等的正根,
两个不等的正根,
令![]() ,
,![]() ,
,![]() ,
,
令![]() ,
,
当![]() 时
时![]() ,此时
,此时![]() 单调递增,
单调递增,![]()
![]() ;
;
当![]() 时
时![]() ,此时
,此时![]() 单调递减,
单调递减,![]()
∴函数![]() 在
在![]() 处取得极大值,也是最大值
处取得极大值,也是最大值![]() ,
,
因为![]() 两个不等的正根,
两个不等的正根,
∴![]() ,得
,得![]() ,
,
∴实数a的取值范围是![]() ;
;
(Ⅲ)∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,令
,令![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,
单调递减,
故![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
故![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某健身机构统计了去年该机构所有消费者的消费金额(单位:元),如下图所示:

(1)将去年的消费金额超过 3200 元的消费者称为“健身达人”,现从所有“健身达人”中随机抽取 2 人,求至少有 1 位消费者,其去年的消费金额超过 4000 元的概率;
(2)针对这些消费者,该健身机构今年欲实施入会制,详情如下表:
会员等级 | 消费金额 |
普通会员 | 2000 |
银卡会员 | 2700 |
金卡会员 | 3200 |
预计去年消费金额在![]() 内的消费者今年都将会申请办理普通会员,消费金额在
内的消费者今年都将会申请办理普通会员,消费金额在![]() 内的消费者都将会申请办理银卡会员,消费金额在
内的消费者都将会申请办理银卡会员,消费金额在![]() 内的消费者都将会申请办理金卡会员. 消费者在申请办理会员时,需-次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
内的消费者都将会申请办理金卡会员. 消费者在申请办理会员时,需-次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
方案 1:按分层抽样从普通会员, 银卡会员, 金卡会员中总共抽取 25 位“幸运之星”给予奖励: 普通会员中的“幸运之星”每人奖励 500 元; 银卡会员中的“幸运之星”每人奖励 600 元; 金卡会员中的“幸运之星”每人奖励 800 元.
方案 2:每位会员均可参加摸奖游戏,游戏规则如下:从-个装有 3 个白球、 2 个红球(球只有颜色不同)的箱子中, 有放回地摸三次球,每次只能摸-个球.若摸到红球的总数消费金额/元为 2,则可获得 200 元奖励金; 若摸到红球的总数为 3,则可获得 300 元奖励金;其他情况不给予奖励. 规定每位普通会员均可参加 1 次摸奖游戏;每位银卡会员均可参加 2 次摸奖游戏;每位金卡会员均可参加 3 次摸奖游戏(每次摸奖的结果相互独立) .
以方案 2 的奖励金的数学期望为依据,请你预测哪-种方案投资较少?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
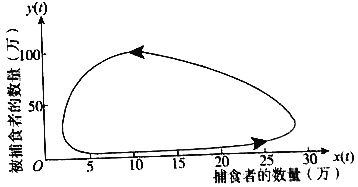
【题目】假设存在两个物种,前者有充足的食物和生存空间,而后者仅以前者为食物,则我们称前者为被捕食者,后者为捕食者.现在我们来研究捕食者与被捕食者之间理想状态下的数学模型.假设捕食者的数量以![]() 表示,被捕食者的数量以
表示,被捕食者的数量以![]() 表示.如图描述的是这两个物种随时间变化的数量关系,其中箭头方向为时间增加的方向.下列说法正确的是( )
表示.如图描述的是这两个物种随时间变化的数量关系,其中箭头方向为时间增加的方向.下列说法正确的是( )
A.若在![]() 、
、![]() 时刻满足:
时刻满足:![]() ,则
,则![]()
B.如果![]() 数量是先上升后下降的,那么
数量是先上升后下降的,那么![]() 的数量一定也是先上升后下降
的数量一定也是先上升后下降
C.被捕食者数量与捕食者数量不会同时到达最大值或最小值
D.被捕食者数量与捕食者数量总和达到最大值时,被捕食者的数量也会达到最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知衡量病毒传播能力的最重要指标叫做传播指数RO.它指的是,在自然情况下(没有外力介入,同时所有人都没有免疫力),一个感染到某种传染病的人,会把疾病传染给多少人的平均数.它的简单计算公式是:![]() 确认病例增长率
确认病例增长率![]() 系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确认病例的平均增长率为
系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确认病例的平均增长率为![]() ,两例连续病例的间隔时间的平均数为
,两例连续病例的间隔时间的平均数为![]() 天,根据以上RO数据计算,若甲得这种传染病,则
天,根据以上RO数据计算,若甲得这种传染病,则![]() 轮传播后由甲引起的得病的总人数约为( )
轮传播后由甲引起的得病的总人数约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com