练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知F1、F2分别是双曲线 ﹣ =1（a＞0，b＞0）的左、右焦点，以坐标原点O为圆心，OF1为半径的圆与双曲线在第一象限的交点为P，则当△PF1F2的面积等于a2时，双曲线的离心率为（ ）
    A.
    B.
    C.
    D.2

    【答案】A
    【解析】解：设F1F2=2c，由题意知△F1F2P是直角三角形，
    ∴F1P2+F2P2=F1F22 ，
    又根据曲线的定义得：
    F1P﹣F2P=2a，
    平方得：F1P2+F2P2﹣2F1P×F2P=4a2
    从而得出F1F22﹣2F1P×F2P=4a2
    ∴F1P×F2P=2（c2﹣a2）
    又当△PF1F2的面积等于a2
    即 F1P×F2P=a2
    2（c2﹣a2）=a2∴c= a，
    ∴双曲线的离心率e= = ．
    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}的各项均为正数，且Sn= + +…+ ，S2= ，S3= ．设[x]表示不大于x的最大整数（如[2.10]=2，[0.9]=0）．
    （1）试求数列{an}的通项；
    （2）求T=[log21]+[log22]+[log23]+…+[log2（ ﹣1）]+[log2（ ）]关于n的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=ax2﹣2ax+b（a≠0）在闭区间[1，2]上有最大值0，最小值﹣1，则a，b的值为（ ）
    A.a=1，b=0
    B.a=﹣1，b=﹣1
    C.a=1，b=0或a=﹣1，b=﹣1
    D.以上答案均不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，且.

    （Ⅰ）求函数的解析式；

    （Ⅱ）若对任意，都有，求的取值范围；

    （Ⅲ）证明函数的图象在图象的下方.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P ABCD中，底面ABCD为平行四边形， ，PA⊥平面ABCD，E为PD的中点．

    （Ⅰ）证明：PB∥平面AEC；

    （Ⅱ）设AD＝2， ，求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个盒子里装有标号为1，2，3，…，5的5张标签，现随机地从盒子里无放回地抽取两张标签．记X为两张标签上的数字之和．
    （1）求X的分布列．
    （2）求X的期望E（X）和方差D（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在五面体ABCDEF中，FA⊥平面ABCD，AD∥BC∥FE，AB⊥AD，M为EC的中点，AF=AB=BC=FE= AD，

    （1）求异面直线BF与DE所成的角的大小；
    （2）证明平面AMD⊥平面CDE；
    （3）求二面角A﹣CD﹣E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工科院校对， 两个专业的男女生人数进行调查，得到如下的列联表：

    专业

    专业

    总计

    女生

    12

    4

    16

    男生

    38

    46

    84

    总计

    50

    50

    100

    （Ⅰ）从专业的女生中随机抽取2名女生参加某项活动，其中女生甲被选到的概率是多少？

    （Ⅱ）能否有95%的把握认为工科院校中“性别”与“专业”有关系？

    附： ．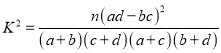

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正方体ABCD﹣A1B1C1D1中，E、F分别是AA1、AB的中点，则EF与对角面A1C1CA所成角的度数是（ ）
    A.30°
    B.45°
    C.60°
    D.150°

    查看答案和解析>>

    同步练习册答案