
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() ,
, ![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 和圆
和圆![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() .
.

【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)先根据面面垂直性质定理得![]() 平面
平面![]() ,即得
,即得![]() ,再根据圆性质得
,再根据圆性质得![]() ,根据线面垂直判定定理得
,根据线面垂直判定定理得![]() 平面
平面![]() ,,最后根据面面垂直判定定理得结论(2)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组求各面法向量,根据向量数量积求向量夹角,最后根据向量夹角与二面角关系建立方程,求出
,,最后根据面面垂直判定定理得结论(2)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组求各面法向量,根据向量数量积求向量夹角,最后根据向量夹角与二面角关系建立方程,求出![]() 的长
的长
试题解析:(Ⅰ)∵平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() 为圆
为圆![]() 的直径,∴
的直径,∴![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]()
(Ⅱ)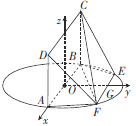
设![]() 中点为
中点为![]() ,以
,以![]() 为坐标原点,
为坐标原点, ![]() 方向分别为
方向分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴方向建立空间直角坐标系(如图).设
轴方向建立空间直角坐标系(如图).设![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,又
,又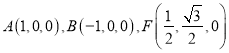 ,∴
,∴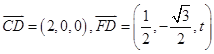 ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,即
,即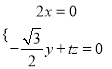 ,
,
令![]() ,解得
,解得![]() .
.
∴![]() .
.
由(1)可知![]() 平面
平面![]() ,取平面
,取平面![]() 的一个法向量为
的一个法向量为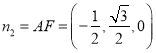 ,
,
∴![]() ,即
,即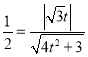 ,解得
,解得![]() ,
,
因此,当![]() 的长为
的长为![]() 时,平面
时,平面![]() 与平面
与平面![]() 所成的锐二面角的大小为60°。
所成的锐二面角的大小为60°。


科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,并说明曲线
的极坐标方程化为直角坐标方程,并说明曲线![]() 的形状;
的形状;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段的长.
截得的线段的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 图象上不同两点
图象上不同两点![]() ,
, ![]() 处切线的斜率分别是
处切线的斜率分别是![]() ,
, ![]() ,规定
,规定![]() (
(![]() 为线段
为线段![]() 的长度)叫做曲线
的长度)叫做曲线![]() 在点
在点![]() 与
与![]() 之间的“弯曲度”,给出以下命题:
之间的“弯曲度”,给出以下命题:
①函数![]() 图象上两点
图象上两点![]() 与
与![]() 的横坐标分别为1和2,则
的横坐标分别为1和2,则![]() ;
;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点![]() ,
, ![]() 是抛物线
是抛物线![]() 上不同的两点,则
上不同的两点,则![]() ;
;
④设曲线![]() (
(![]() 是自然对数的底数)上不同两点
是自然对数的底数)上不同两点![]() ,
, ![]() ,且
,且![]() ,若
,若![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是![]() .
.
其中真命题的序号为__________.(将所有真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(365天)内100天的空气质量指数![]() (Air Pollution Index)的监测数据,结果统计如下:
(Air Pollution Index)的监测数据,结果统计如下:
|
|
|
|
|
|
| 大于300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重 污染 | 重度污染 |
天数 | 10 | 15 | 20 | 30 | 7 | 6 | 12 |
(Ⅰ)若本次抽取的样本数据有30天是在供暖季,其中有7天为重度污染,完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 5.024 | 6.635 | 7.879 | 10.828 |
附: 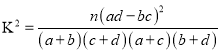
(Ⅱ)政府要治理污染,决定对某些企业生产进行管控,当![]() 在区间
在区间![]() 时企业正常生产;当
时企业正常生产;当![]() 在区间
在区间![]() 时对企业限产
时对企业限产![]() (即关闭
(即关闭![]() 的产能),当
的产能),当![]() 在区间
在区间![]() 时对企业限产
时对企业限产![]() ,当
,当![]() 在300以上时对企业限产
在300以上时对企业限产![]() ,企业甲是被管控的企业之一,若企业甲正常生产一天可得利润2万元,若以频率当概率,不考虑其他因素:
,企业甲是被管控的企业之一,若企业甲正常生产一天可得利润2万元,若以频率当概率,不考虑其他因素:
①在这一年中随意抽取5天,求5天中企业被限产达到或超过![]() 的恰为2天的概率;
的恰为2天的概率;
②求企业甲这一年因限产减少的利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题12分)如图,在海岸线![]() 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段
一侧有一休闲游乐场,游乐场的前一部分边界为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
,![]() 的图像,图像的最高点为
的图像,图像的最高点为![]() .边界的中间部分为长
.边界的中间部分为长![]() 千米的直线段
千米的直线段![]() ,且
,且![]() .游乐场的后一部分边界是以
.游乐场的后一部分边界是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.

(1)求曲线段![]() 的函数表达式;
的函数表达式;
(2)曲线段![]() 上的入口
上的入口![]() 距海岸线
距海岸线![]() 最近距离为
最近距离为![]() 千米,现准备从入口
千米,现准备从入口![]() 修一条笔直的景观路到
修一条笔直的景观路到![]() ,求景观路
,求景观路![]() 长;
长;
(3)如图,在扇形![]() 区域内建一个平行四边形休闲区
区域内建一个平行四边形休闲区![]() ,平行四边形的一边在海岸线
,平行四边形的一边在海岸线![]() 上,一边在半径
上,一边在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求平行四边形休闲区
,求平行四边形休闲区![]() 面积的最大值及此时
面积的最大值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,其焦距为2,离心率为
,其焦距为2,离心率为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆的右焦点为![]() ,
, ![]() 为
为![]() 轴上一点,满足
轴上一点,满足![]() ,过点
,过点![]() 作斜率不为0的直线
作斜率不为0的直线![]() 交椭圆于
交椭圆于![]() 两点,求
两点,求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )

A. 6 B. 8
C. 12 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com