
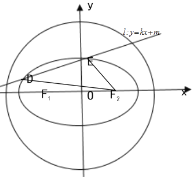
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且![]() .
.
(1)求椭圆C的方程.
(2)不经过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长与椭圆C的长轴长相等,且直线
截得的弦长与椭圆C的长轴长相等,且直线![]() 与椭圆C交于D,E两点,试判断
与椭圆C交于D,E两点,试判断![]() 的周长是否为定值?若是,求出定值;若不是,请说明理由.
的周长是否为定值?若是,求出定值;若不是,请说明理由.
【答案】(1)![]() (2)
(2)![]() 的周长为定值为
的周长为定值为![]() ,详见解析
,详见解析
【解析】
(1)根据已知条件求出A、B两点的坐标,再由![]() 和离心率为
和离心率为![]() 建立关于a,b,c的方程,从而得椭圆的方程;
建立关于a,b,c的方程,从而得椭圆的方程;
(2)根据直线被圆所截得的弦长等于椭圆的长轴长得出k,m的关系,再将直线与椭圆的方程联立消去y,得到交点的横坐标的韦达定理表达式,分别求出![]() ,得出
,得出![]() 的周长为定值,得解.
的周长为定值,得解.
(1)因为![]() ,所以
,所以![]() ,则
,则![]() 即
即![]() ,所以椭圆C的方程可化为
,所以椭圆C的方程可化为![]() ,
,
由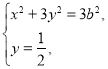 得
得![]() 不妨令
不妨令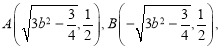
易知![]() 则
则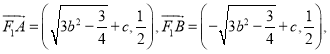
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]()
所以椭圆C的方程为![]()
(2)由(1)知椭圆C的长轴长为![]() ,因为直线
,因为直线![]() 被圆
被圆![]() 截得的弦长与椭圆C的长轴长相等,所以圆
截得的弦长与椭圆C的长轴长相等,所以圆![]() 的圆心O(O为坐标原点)到直线l的距离
的圆心O(O为坐标原点)到直线l的距离![]() ,所以
,所以![]() ,即
,即![]()
设![]() ,联立方程,得
,联立方程,得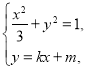 整理得
整理得![]()
![]()
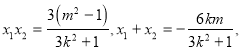
所以![]() ,又
,又![]() ,
,
所以![]()
又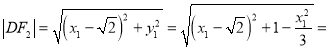
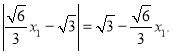
![]()
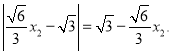
所以![]() ,
,
所以![]() 的周长是
的周长是![]() .
.
所以![]() 的周长为定值,为
的周长为定值,为![]() .
.
得解.


科目:高中数学 来源: 题型:
【题目】设函数![]() 、
、![]() 满足关系
满足关系![]() ,其中
,其中![]() 是常数.
是常数.
(1)设![]() ,
,![]() ,求
,求![]() 的解析式;
的解析式;
(2)是否存在函数![]() 及常数
及常数![]() (
(![]() )使得
)使得![]() 恒成立?若存在,请你设计出函数
恒成立?若存在,请你设计出函数![]() 及常数
及常数![]() ;不存在,请说明理由;
;不存在,请说明理由;
(3)已知![]() 时,总有
时,总有![]() 成立,设函数
成立,设函数![]() (
(![]() )且
)且![]() ,对任意
,对任意![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是由正整数构成的数表,用aij表示i行第j个数(i,j∈N+).此表中ail=aii=i,每行中除首尾两数外,其他各数分别等于其“肩膀”上的两数之和.

(1)写出数表的第六行(从左至右依次列出).
(2)设第n行的第二个数为bn(n≥2),求bn.
(3)令![]() ,记Tn为数列
,记Tn为数列![]() 前n项和,求
前n项和,求![]() 的最大值,并求此时n的值.
的最大值,并求此时n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 命题“若![]() ,则
,则![]() ”的逆命题是真命题
”的逆命题是真命题
B. 命题“存在![]() ”的否定是:“任意
”的否定是:“任意![]() ”
”
C. 命题“p或q”为真命题,则命题“p”和命题“q”均为真命题
D. 已知![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:平均每天喝500![]() 以上为常喝,体重超过50
以上为常喝,体重超过50![]() 为肥胖.
为肥胖.
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中有2名女生,现从常喝碳酸饮料且肥胖的学生抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下面四个命题,其中正确命题的序号是( )
①“直线![]() 、
、![]() 不相交”是“直线
不相交”是“直线![]() 、
、![]() 为异面直线”的充分而不必要条件;②“直线
为异面直线”的充分而不必要条件;②“直线![]() 平面
平面![]() 内所有直线”的充要条件是“
内所有直线”的充要条件是“![]() 平面
平面![]() ”;③“直线
”;③“直线![]() 直线
直线![]() ”的充要条件是“
”的充要条件是“![]() 平行于
平行于![]() 所在的平面”;④“直线
所在的平面”;④“直线![]() 平面
平面![]() ”的必要而不充分条件是“直线
”的必要而不充分条件是“直线![]() 平行于
平行于![]() 内的一条直线.”
内的一条直线.”
A.①③B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
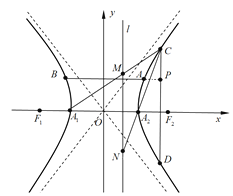
【题目】已知双曲线![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,左、右两顶点分别是
,左、右两顶点分别是![]() 、
、![]() ,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点
,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点![]() 如图).
如图).
⑴若![]() 是
是![]() 的一条渐近线的一个方向向量,试求
的一条渐近线的一个方向向量,试求![]() 的两渐近线的夹角
的两渐近线的夹角![]() ;
;
⑵若![]() ,
,![]() ,
,![]() ,
,![]() ,试求双曲线
,试求双曲线![]() 的方程;
的方程;
⑶在⑴的条件下,且![]() ,点C与双曲线的顶点不重合,直线
,点C与双曲线的顶点不重合,直线![]() 和直线
和直线![]() 与直线l:
与直线l:![]() 分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若存在常数M,使得对任意
,若存在常数M,使得对任意![]() ,
,![]() 与
与![]() 中至少有一个不小于M,则记作
中至少有一个不小于M,则记作![]() ,那么下列命题正确的是( ).
,那么下列命题正确的是( ).
A.若![]() ,则数列
,则数列![]() 各项均大于或等于M;
各项均大于或等于M;
B.若![]() ,则
,则![]() ;
;
C.若![]() ,
,![]() ,则
,则![]() ;
;
D.若![]() ,则
,则![]() ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com