
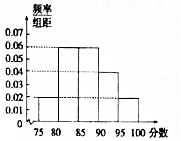
 某校为了了解高三学生体育达标情况,在高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某校为了了解高三学生体育达标情况,在高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:分析 (1)设“学生甲被选中复查”为事件A,根据分层抽样的方法求出每组的人数,即可求出P(A);
(2)记第3组选中的3人分别是a,b,c,第4组选中的2人分别为x,y,第五组选中的人为m,用列举法计算基本事件数,求出概率即可.
解答 解:(1)设“学生甲被选中复查”为事件A,
第三组人数为50×0.06×5=15,
第四组人数为50×0.04×5=10,
第五组人数为50×0.02×5=5,
根据分层抽样知,第三组应抽取3人,第四组应抽取2人,第五组应抽取1人,
所以P(A)=$\frac{1}{5}$;
(2)记第三组选中的三人分别是a,b,c,第四组选中的二人分别为x,y,第五组选中的人为m,
从这六人中选出两人,有以下基本事件:
ab,ac,ax,ay,am,bc,bx,by,bm,cx,cy,cm,xy,xm,ym,共15个基本事件,
符合1人在第3组1人在第4组的基本事件有ax,ay,bx,by,cx,cy,共6个,
故所求的概率为P=$\frac{6}{15}$=$\frac{2}{5}$.
点评 本题考查了分层抽样以及列举法求概率的应用问题,属于基础题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是偶函数 | B. | f(x)最小正周期为2π | ||
| C. | f(x)图线关于直线点x=-$\frac{π}{6}$对称 | D. | f(x)图象关于点(-$\frac{π}{6}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行平移$\frac{π}{2}$个单位长度 | B. | 向右平行平移$\frac{π}{4}$个单位长度 | ||
| C. | 向右平行平移$\frac{π}{2}$个单位长度 | D. | 向左平行平移$\frac{π}{4}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n2 | B. | (n-1)2 | C. | n(n-1) | D. | n(n+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
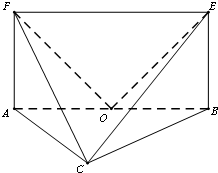 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 100 | C. | -101 | D. | -99 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com