
【题目】(2015·四川)设直线l与抛物线y2=4x相交于A,B两点,与圆(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是( )
A.(1,3)
B.(1, 4)
C.(2,3)
D.(2,4)
【答案】D
【解析】显然当直线f的斜率不存在时,必有两条直线满足题设.当直线l的斜率存在时,设斜率为k .设A(x1, y1), B(x2, y2), x1≠x2 , M(x0, y0), 则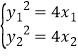 ,相减得(y1+y2)(y1-y2)=4(x1-x2), 由于x1≠x2 , 所以
,相减得(y1+y2)(y1-y2)=4(x1-x2), 由于x1≠x2 , 所以![]() , 即ky0=2, 圆心为C(5,0),由CM⊥AB,得k·
, 即ky0=2, 圆心为C(5,0),由CM⊥AB,得k·![]() =-1, ky0=5- x0. 所以2=5- x0 , x0=3, 即点M必在直线x=3上将x=3代入y2=4x得y2=12, ∴-2
=-1, ky0=5- x0. 所以2=5- x0 , x0=3, 即点M必在直线x=3上将x=3代入y2=4x得y2=12, ∴-2![]() <y0<2
<y0<2![]() . 因为点M在圆(x-5)2+y2=r2(r>0)上, 所以(x0-5)2+y02=r2 , r2=y02+4<12+4=16, 又y02+4>4(由于斜率不存在, 故y0≠0, 所以不取等号),所以4<y02+4<16, 所以2<r<4, 选D。
. 因为点M在圆(x-5)2+y2=r2(r>0)上, 所以(x0-5)2+y02=r2 , r2=y02+4<12+4=16, 又y02+4>4(由于斜率不存在, 故y0≠0, 所以不取等号),所以4<y02+4<16, 所以2<r<4, 选D。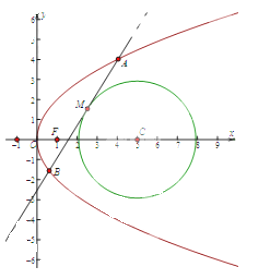
首先应结合图形进行分析.结合图形易知,只要圆的半径小于5,那么必有两条直线(即与x轴 垂直的两条切线)满足题设,因此只需直线的斜率存在时,再有两条直线满足题设即可.接下来要解决的问题是当直线的斜率存在时,圆的半径的范围是什么.涉及 直线与圆锥曲线的交点及弦的中点的问题,常常采用“点差法”.在本题中利用点差法可得,中点必在直线x=3上,由此可确定中点的纵坐标y0的范围,利用这个范围即可得到r的取值范围.


科目:高中数学 来源: 题型:
【题目】![]() 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记![]() BOP=x,将动P到A、B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()
BOP=x,将动P到A、B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()
A.
B.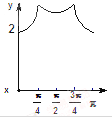
C.
D.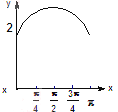
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)在直角坐标系xoy中,曲线C:y=![]() 与直线y=kx+a(a>0)交与M,N两点,
与直线y=kx+a(a>0)交与M,N两点,
(1)当k=0时,分别求C在点M和N处的切线方程;
(2)y轴上是否存在点P , 使得当k变动时,总有∠OPM=∠OPN?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 的对边分别为
的对边分别为![]() 且
且![]() 为锐角,问:(1)证明: B - A =
为锐角,问:(1)证明: B - A = ![]() ,(2)求 sin A + sin C 的取值范围
,(2)求 sin A + sin C 的取值范围
(1)(1)证明:![]()
(2)(2)求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)一辆小客车上有5个座位,其座位号为1,2,3,4,5,乘客P1 , P2 , P3 , P4 , P5的座位号分别为1,2,3,4,5,他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(1)(I)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
乘客 | P1 | P2 | P3 | P4 | P5 |
座位号 | 3 | 2 | 1 | 4 | 5 |
3 | 2 | 4 | 5 | 1 | |
(2)(Ⅱ)若乘客P1坐到了2号座位,其他乘客按规则就坐,求乘客P1坐到5号座位的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为![]() ,则cos
,则cos![]() 的最大值为 .
的最大值为 .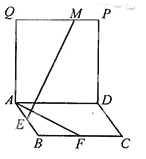
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马P-ABCD中,侧棱![]() 底面
底面![]() ,且
,且![]() ,过棱
,过棱![]() 的中点
的中点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]()
(1)证明:![]() 平面
平面![]() .试判断四面体
.试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写
是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
(2)若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com