
【题目】某工厂加工一批零件,加工过程中会产生次品,根据经验可知,其次品率p与日产量x(万件)之间满足函数关系式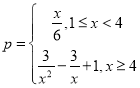 ,已知每生产1万件合格品可获利2万元,但生产1万件次品将亏损1万元(次品率=次品数/生产量)
,已知每生产1万件合格品可获利2万元,但生产1万件次品将亏损1万元(次品率=次品数/生产量)
(1)试写出加工这批零件的日盈利额y(万元)与日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?最大利润为多少?
科目:高中数学 来源: 题型:
【题目】对任意x∈R,存在函数f(x)满足( )
A.f(cosx)=sin2xB.f(sin2x)=sinx
C.f(sinx)=sin2xD.f(sinx)=cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在本题中,我们把具体如下性质的函数![]() 叫做区间
叫做区间![]() 上的闭函数:①
上的闭函数:①![]() 的定义域和值域都是
的定义域和值域都是![]() ;②
;②![]() 在
在![]() 上是增函数或者减函数.
上是增函数或者减函数.
(1)若![]() 在区间
在区间![]() 上是闭函数,求常数
上是闭函数,求常数![]() 的值;
的值;
(2)找出所有形如![]() 的函数(
的函数(![]() 都是常数),使其在区间
都是常数),使其在区间![]() 上是闭函数.
上是闭函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现给出两个条件:①![]() ,②
,②![]() ,从中选出一个条件补充在下面的问题中,并以此为依据求解问题:(选出一种可行的条件解答,若两个都选,则按第一个解答计分)在
,从中选出一个条件补充在下面的问题中,并以此为依据求解问题:(选出一种可行的条件解答,若两个都选,则按第一个解答计分)在![]() 中,
中,![]() 分别为内角
分别为内角![]() 所对的边( ).
所对的边( ).
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴为正半轴为极轴建立极坐标系.已知曲线
轴为正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 过定点
过定点![]() 且倾斜角为
且倾斜角为![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)把曲线![]() 化成直角坐标方程,并求
化成直角坐标方程,并求![]() 的值;
的值;
(2)若![]() 成等比数列,求直线
成等比数列,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)椭圆![]()
![]() (
(![]() )的上顶点为
)的上顶点为![]() ,
, ![]() 是
是![]() 上的一点,以
上的一点,以![]() 为直径的圆经过椭圆
为直径的圆经过椭圆![]() 的右焦点
的右焦点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,问:在
有且只有一个公共点,问:在![]() 轴上是否存在两个定点,它们到直线
轴上是否存在两个定点,它们到直线![]() 的距离之积等于
的距离之积等于![]() ?如果存在,求出这两个定点的坐标;如果不存在,说明理由.
?如果存在,求出这两个定点的坐标;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com