Question

【题目】如图，已知长方形中，，，M为DC的中点.将沿折起，使得平面⊥平面.

（1）求证：；

（2）若点是线段上的一动点，问点在何位置时，二面角的余弦值为.

Answer 1

【答案】（1）详见解析；（2）E为DB中点。

【解析】

试题分析：

（1）本问考查立体几何中的折叠问题，考查学生的读图能力及空间想象能力，由长方形ABCD中,，所以，同理可求出，这样可以根据数量关系证出，即，由于折叠到平面ADM⊥平面ABCM，交线为AM，根据面面垂直的性质定理可知，由于，且平面ABM，所以平面ADM，又因为平面ADM，所以；本问主要考查面面垂直性质定理的应用，注意定理的使用条件，注意证明的书写格式。

（2）根据平面ADM⊥平面ABCM，交线为AM，且AD=DM，可以取AM中点O，连接DO，则DO⊥AM，根据面面垂直性质定理可知，DO⊥平面ABCM，再取AB中点N，连接ON，则ON//BM，所以ON⊥AM，可以以O为原点，OA,ON,OD所在直线分别为x,y,z轴建立空间直角坐标系，如图，求出A,M,D,B点坐标，根据E在BD上，设，求出E点坐标，然后分别求出平面AMD和平面AME的法向量，从而将二面角的余弦值表示成两个法向量余弦值，求出的值，得到E点的位置。

试题解析：

（1）证明：∵长方形ABCD中，AB=，AD=，M为DC的中点，

∴AM=BM=2，∴BM⊥AM.

∵平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，BM平面ABCM

∴BM⊥平面ADM

∵AD平面ADM

∴AD⊥BM.

（2）建立如图所示的直角坐标系

设，则平面AMD的一个法向量，

，

设平面AME的一个法向量 则 取y=1，得

所以，

因为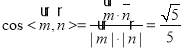，求得，

所以E为BD的中点.