
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 的图象关于点
的图象关于点![]() 对称②
对称②![]() 的最大值为
的最大值为![]()
③![]() 在区间
在区间![]() 上单调递增④
上单调递增④![]() 是周期函数且最小正周期为
是周期函数且最小正周期为![]()
其中所有正确结论的编号是( )
A.①②B.①③C.①④D.②④
科目:高中数学 来源: 题型:
【题目】德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
合格的概率 |
|
|
|
|
(1)求甲同学取得参加数学竞赛复赛的资格的概率;
(2)记![]() 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
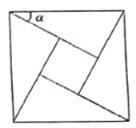
【题目】“剑桥学派”创始人之一数学家哈代说过:“数学家的造型,同画家和诗人一样,也应当是美丽的”;古希腊数学家毕达哥拉斯创造的“黄金分割”给我们的生活处处带来美;我国古代数学家赵爽创造了优美“弦图”.“弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的椭圆![]() 和抛物线
和抛物线![]() 有相同的焦点
有相同的焦点![]() ,椭圆
,椭圆![]() 过点
过点![]() ,抛物线
,抛物线![]() 的顶点为原点.
的顶点为原点.
![]() 求椭圆
求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
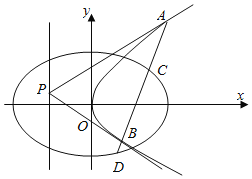
![]() 设点P为抛物线
设点P为抛物线![]() 准线上的任意一点,过点P作抛物线
准线上的任意一点,过点P作抛物线![]() 的两条切线PA,PB,其中A,B为切点.
的两条切线PA,PB,其中A,B为切点.
![]() 设直线PA,PB的斜率分别为
设直线PA,PB的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 为定值;
为定值;
![]() 若直线AB交椭圆
若直线AB交椭圆![]() 于C,D两点,
于C,D两点,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的面积,试问:
的面积,试问:![]() 是否有最小值?若有,求出最小值;若没有,请说明理由.
是否有最小值?若有,求出最小值;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有以下三个判断
有以下三个判断
①函数恒有两个零点且两个零点之积为-1;
②函数恒有两个极值点且两个极值点之积为-1;
③若![]() 是函数的一个极值点,则函数极小值为-1.
是函数的一个极值点,则函数极小值为-1.
其中正确判断的个数有( )
A.0个B.1个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为![]() ,AC,
,AC,![]() ,
,![]() 的中点,AB=BC=
的中点,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求证:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)证明:直线FG与平面BCD相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个有穷数列每相邻两项之间添加一项,使其等于两相邻项的和,我们把这样的操作叫做该数列的一次“H扩展”. 已知数列1,2. 第一次“H扩展”后得到1,3,2;第二次“H扩展”后得到1,4,3,5,2; 那么第10次“H扩展”后得到的数列的所有项的和为( )
A.88572B.88575C.29523D.29526
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com