
����Ŀ��ij�����߿�ʵ���·������涨�����ġ���ѧ��Ӣ���ǿ����ıؿ���Ŀ�������������������ѧ����������ʷ������������������Ŀ��ѡȡ������Ŀ��Ϊѡ����Ŀ����һ��ѧ����������Ŀ��ѡ����������Ŀ��Ϊѡ����Ŀ����Ƹ�ѧ����ѡ������ȷ�����������Ƹ�ѧ��ѡ��������ȷ����������ѧ����ѡ����������ѧ���������ѡ����Ŀ����ѧ����ѡ������ȷ��������������ѧ�����Ϊ��ѡ��������
ijѧУΪ�˽��һ�꼶420��ѧ��ѡ����Ŀ�����������ѡȡ30��ѧ��������һ�ε�����ͳ��ѡ����Ŀ�������±���
�Ա� | ѡ������ȷ����� | ���� | ��ѧ | ���� | ��ʷ | ���� | ���� |
���� | ѡ������ȷ������8�� | 8 | 8 | 4 | 2 | 1 | 1 |
ѡ��������ȷ������6�� | 4 | 3 | 0 | 1 | 0 | 0 | |
Ů�� | ѡ������ȷ������10�� | 8 | 9 | 6 | 3 | 3 | 1 |
ѡ��������ȷ������6�� | 5 | 4 | 1 | 0 | 0 | 1 |
�������Ƹ�ѧУ��һ�꼶ѡ������ȷ����ѧ����ѡ�������ѧ���ж�����?
��������������Ů��ѡ��ѡ����Ŀ�������������ѡ������ȷ����8λ���������ѡ��1������ѡ������ȷ����10λŮ�������ѡ��1���������������Ů����ѡ�������ж�������ʷѧ�Ƶĸ��ʣ�
������ѡ������ȷ����8�����������ѡ��2�������������![]() ����
����![]() ��
��
���𰸡�����![]() ������
������![]() ����
����![]() ��
��
��������
�������������������˼�룬�ȼ���������Ƶ�ʣ��ٳ����������ɵý⣻
���ֱ����������Ů������ʷ�ĸ��ʣ���˼��ɣ�
�����ȷ�������8��������ѡ������������ùŵ������⼴��.
���������֪��ѡ������ȷ����������ȷ��ѡ�������ѧ����4�ˣ�ѡ������ȷ����Ů����ȷ��ѡ�������ѧ����6�ˣ���ѧУ��һ�꼶ѡ������ȷ����ѧ����ѡ�������ѧ����![]() �ˣ�
�ˣ�
���������ݿ�֪��ѡ������ȷ����8λ������ѡ��1��ѡ�������к�����ʷѧ�Ƶĸ���Ϊ![]() ��ѡ������ȷ����10λŮ����ѡ��1�˺�����ʷѧ�Ƶĸ���Ϊ
��ѡ������ȷ����10λŮ����ѡ��1�˺�����ʷѧ�Ƶĸ���Ϊ![]() �����Ը�������Ů����ѡ�������ж�������ʷѧ�Ƶĸ���Ϊ
�����Ը�������Ů����ѡ�������ж�������ʷѧ�Ƶĸ���Ϊ![]() ��
��
���������ݿ�ѡ��ѡ������ȷ������������4��ѡ����������ѧ�������2��ѡ����������ѧ����ʷ����1��ѡ��������ѧ�͵�������1��ѡ����������ѧ�����Σ�
![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
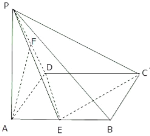
����Ŀ����ͼ,ABCD�DZ߳�Ϊ3��������,DE��ƽ��ABCD,AF��DE,DE=3AF,BE��ƽ��ABCD���ɽ�Ϊ60��.
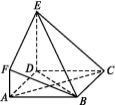
(1)������F-BE-D������ֵ;
(2)���M���߶�BD��һ������,��ȷ����M��λ��,ʹ��AM��ƽ��BEF,��֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У�
��![]() ��
��![]() .
.
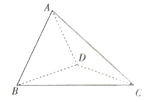
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�о�ij��ͼ��ÿ��ijɱ���![]() ��Ԫ����ӡˢ��
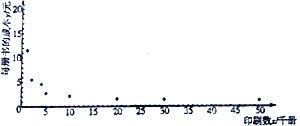
��Ԫ����ӡˢ��![]() ��ǧ�ᣩ�Ĺ�ϵ���ռ���һЩ���ݲ����˳����������õ��������ɢ��ͼ��һЩͳ������ֵ��
��ǧ�ᣩ�Ĺ�ϵ���ռ���һЩ���ݲ����˳����������õ��������ɢ��ͼ��һЩͳ������ֵ��
|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
����![]() ��
�� ![]() ��
��
��1������ɢ��ͼ�жϣ� ![]() ��
��![]() ��һ����������Ϊÿ��ɱ���
��һ����������Ϊÿ��ɱ���![]() ��Ԫ����ӡˢ��
��Ԫ����ӡˢ��![]() ��ǧ�ᣩ�Ļع鷽�����ͣ���ֻҪ������жϣ�����˵�����ɣ�
��ǧ�ᣩ�Ļع鷽�����ͣ���ֻҪ������жϣ�����˵�����ɣ�
��2�����ݣ�1�����жϽ�����������ݣ�����![]() ����
����![]() �Ļع鷽�̣��ع�ϵ���Ľ����ȷ��0.01����
�Ļع鷽�̣��ع�ϵ���Ľ����ȷ��0.01����
��3����ÿ���鶨��Ϊ10Ԫ��������Ӧ��ӡˢ���ٲ����ʹ����������78840Ԫ���������ܹ�ȫ���۳��������ȷ��1��
����������һ������![]() ��
�� ![]() ������
������ ![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ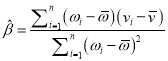 ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ����������ԭ��
Ϊ����������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ����
����![]() ��.
��.
��1��д������![]() �ļ����귽�̣�����
�ļ����귽�̣�����![]() ��
��![]() ����ļ����ꣻ
����ļ����ꣻ
��2������![]() ������
������![]() ��
��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ����ԭ�㣩����
����ԭ�㣩����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������ס������ֲ�Ʒÿ�������ú����Ͳ�ֵ���±���ʾ.
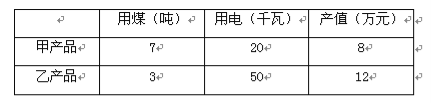
������ÿ�������ó���ú��������, ÿ�칩ú����56�֣���������450ǧ�ߣ��ʸó���ΰ���������ʹ�øó��ղ�ֵ�������ղ�ֵΪ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˶���������������õ��Ӳ�������⣬�����������ĵȼ�Ϊ0-25![]() ���ֱ��������涨����ֵ������
���ֱ��������涨����ֵ������![]() Ϊ�dz����㣬����ֵ������
Ϊ�dz����㣬����ֵ������![]() Ϊ���㣮ij��50��ͬѧ���������������ԣ����ò���ֵ�Ƴ�Ƶ�ʷֲ�ֱ��ͼ��
Ϊ���㣮ij��50��ͬѧ���������������ԣ����ò���ֵ�Ƴ�Ƶ�ʷֲ�ֱ��ͼ��
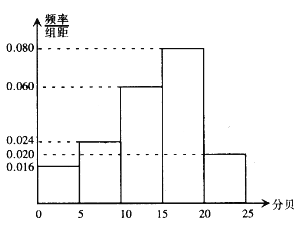
�����ִ������ȼ�Ϊ![]() ��ͬѧ�������ȡ��4�ˣ��������dz������ͬѧ����Ϊ
��ͬѧ�������ȡ��4�ˣ��������dz������ͬѧ����Ϊ![]() ����
����![]() �ķֲ�������ѧ������
�ķֲ�������ѧ������
�����ڣ����г����4������ѡһ�˲μ�һ����������������ԣ����Թ������£��ĸ�����ķ��������ͬ����ǿ�����Ĵ���ֱ�Ϊ1,2,3,4������ǰ������������У������Ե�ͬѧ�����������ĸ����水������ǿ�����һ�����![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ������
������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() Ϊ1,2,3,4��һ�����У�����
Ϊ1,2,3,4��һ�����У�����![]() Ϊ��������ƫ��̶ȵ�һ��������
Ϊ��������ƫ��̶ȵ�һ�������� ![]() ����
����![]() �ĸ��ʣ�
�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() �У�����ABCD�Ǿ��Σ�
�У�����ABCD�Ǿ��Σ�![]() ��ƽ��
��ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ���е㣬
���е㣬![]() ���߶�
���߶�![]() �ϵĵ㣮
�ϵĵ㣮
(1)��![]() ��
��![]() ���е�ʱ����֤��
���е�ʱ����֤��![]() ��ƽ��
��ƽ��![]() ��
��
(2)��![]() ��
��![]() = 2��1ʱ��������
= 2��1ʱ��������![]() ��
��![]() ��
��![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��֪��Բ�������������ֱ���(-2,0)��(2,0)�����Ҿ�����![]() �������ı����̣�
�������ı����̣�
��2����֪˫�����������������ֱ���(0,-6)��(0,6)�����Ҿ�����(2,-5)�������ı�����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com