【题目】如图，已知多面体
中，
为菱形，
，
平面，
，
，
.
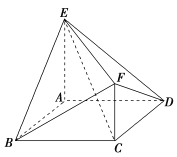
（1）求证：平面
平面
；
（2）求二面角
的余弦值.
【答案】(1)证明见解析；(2)
.
【解析】
（1）由题意可知
、
、
、
共面.连接
，
，相交于点
，由空间几何关系可证得
平面
，则
，结合题意有
平面
，结合面面垂直的判断定理可得平面
平面.
（2）取
的中点
，以A点为坐标原点建立空间直角坐标系，结合几何体的结构特征可得平面
的法向量为
，平面
的法向量
，利用空间向量的结论可得二面角
的余弦值为
.
（1）证明：∵
，∴四点、、、共面.
如图所示，连接，，相交于点，
∵四边形
是菱形，∴对角线
，
∵
平面，
∴
，又
，
∴平面，
∴，
又
，
，
∴平面，
平面
，
∴平面平面.
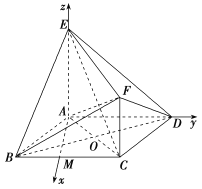
（2）取的中点，
∵
，
，
∴
是等边三角形，∴
，
又
，∴
，
以A点为坐标原点建立如图所示的空间直角坐标系，
则
，
，
，
，
.
，
，
，
.
∵.
∴
，解得
.
设平面的法向量为
，
则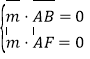
，∴
，
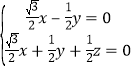取.
同理可得：平面的法向量.
∴
.
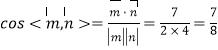由图可知：二面角的平面角为钝角，
∴二面角的余弦值为.
浙江名校名师金卷系列答案
全优冲刺100分系列答案科目：高中数学 来源： 题型：
【题目】已知
为椭圆E： 
的左、右顶点， 
，E的两个焦点与E的短轴两个端点所构成的四边形是正方形．
（1）求椭圆E的方程；
（2）设动点
（
），记直线
与E的交点（不同于
）到x轴的距离分别为
，求
的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数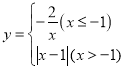
的图象与性质．列表：
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示．
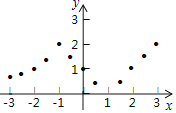
（1）如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；
（2）研究函数并结合图象与表格，回答下列问题：
①点
，
，
，
在函数图象上，
，
；（填“＞”，“＝”或“＜”）
②当函数值
时，求自变量x的值；
③在直线
的右侧的函数图象上有两个不同的点
，
，且
，求
的值；
④若直线
与函数图象有三个不同的交点，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知下列命题：
①在某项测量中，测量结果
服从正态分布
，若在
内取值范围概率为
，则在
内取值的概率为
；
②若
，
为实数，则“
”是“
”的充分而不必要条件；
③已知命题
，
，则
是：
，
；
④
中，“角
，
，
成等差数列”是“
”的充分不必要条件；其中，所有真命题的个数是（ ）
A. 
个 B. 
个 C. 
个 D. 
个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，第1个图形由正三角形扩展而成，共12个顶点.第n个图形是由正n+2边形扩展而来 
，则第n+1个图形的顶点个数是 ( )
（1） 
（2）
（3） 
（4）
A. (2n+1)(2n+2)B. 3(2n+2)C. (n+2)(n+3)D. (n+3)(n+4)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合A={x|ax2+2x+1=0，a∈R}，
（1）若A只有一个元素，试求a的值，并求出这个元素；
（2）若A是空集，求a的取值范围；
（3）若A中至多有一个元素，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在R上的偶函数f(x)满足f(x＋1)＝－f(x)且f(x)在[－1,0]上是增函数，给出下列四个命题：
①f(x)是周期函数；②f(x)的图象关于x＝1对称；③f(x)在[1,2]上是减函数；④f(2)＝f(0)．
其中正确命题的序号是____________．(请把正确命题的序号全部写出来)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
