练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】公元263年左右，我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率，他从单位圆内接正六边形算起，令边数一倍一倍地增加，即12，24，48，…，192，…，逐个算出正六边形，正十二边形，正二十四边形，…，正一百九十二边形，…的面积，这些数值逐步地逼近圆面积，刘徽算到了正一百九十二边形，这时候的近似值是3.141024，刘徽称这个方法为“割圆术”，并且把“割圆术”的特点概括为“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的，用有限来逼近无穷，这种思想极其重要，对后世产生了巨大影响.按照上面“割圆术”，用正二十四边形来估算圆周率，则的近似值是( )（精确到）.（参考数据）

    A.3.14B.3.11C.3.10D.3.05

    【答案】B

    【解析】

    圆内接正二十四边形的中心即为圆心，连接圆心与正二十四边形的各个顶点，构成24个全等的等腰三角形，并且等腰三角形的腰长为单位圆的半径，顶角为，根据圆面积，利用三角形面积公式，计算正二十四边形的面积，求解即可.

    由题意可知，单位圆面积，正二十四边形的面积.

    则.

    即.

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知双曲线：（），直线：，与交于P、Q两点，为P关于y轴的对称点，直线与y轴交于点；

    （1）若点是的一个焦点，求的渐近线方程；

    （2）若，点P的坐标为，且，求k的值；

    （3）若，求n关于b的表达式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    （1）求函数的单调区间；

    （2）使不等式对任意，恒成立时最大的记为，求当时，的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，，设的内切圆分别与边相切于点，已知，记动点的轨迹为曲线.

    (1)求曲线的方程;

    (2)过的直线与轴正半轴交于点，与曲线E交于点轴，过的另一直线与曲线交于两点，若，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（a＞0）.

    （1）求f（x）的单调增区间；

    （2）当x∈[0，π]时，f（x）值域为[3，4]，求a，b的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，曲线在点处的切线方程为.

    （Ⅰ）求，的值；

    （Ⅱ）当时，若为整数，且，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】东莞的轻轨给市民出行带来了很大的方便，越来越多的市民选择乘坐轻轨出行，很多市民都会开汽车到离家最近的轻轨站，将车停放在轻轨站停车场，然后进站乘轻轨出行，这给轻轨站停车场带来很大的压力．某轻轨站停车场为了解决这个问题，决定对机动车停车施行收费制度，收费标准如下：4小时内（含4小时）每辆每次收费5元；超过4小时不超过6小时，每增加一小时收费增加3元；超过6小时不超过8小时，每增加一小时收费增加4元，超过8小时至24小时内（含24小时）收费30元；超过24小时，按前述标准重新计费．上述标准不足一小时的按一小时计费．为了调查该停车场一天的收费情况，现统计1000辆车的停留时间（假设每辆车一天内在该停车场仅停车一次），得到下面的频数分布表：

    （小时）

    频数（车次）

    100

    100

    200

    200

    350

    50

    以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率．

    （1）现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研，记录并统计了停车时长与司机性别的列联表：

    男

    女

    合计

    不超过6小时

    30

    6小时以上

    20

    合计

    100

    完成上述列联表，并判断能否有90%的把握认为“停车是否超过6小时”与性别有关？

    （2）（i）表示某辆车一天之内（含一天）在该停车场停车一次所交费用，求的概率分布列及期望；

    （ii）现随机抽取该停车场内停放的3辆车，表示3辆车中停车费用大于的车辆数，求的概率．

    参考公式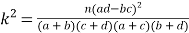：，其中

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.780

    1.323

    2.072

    2.706

    3.841

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若在区间内有且只有一个实数，使得成立，则称函数在区间内具有唯一零点.

    （1）判断函数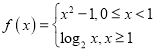在区间内是否具有唯一零点，说明理由：

    （2）已知向量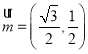，，，证明在区间内具有唯一零点.

    （3）若函数在区间内具有唯一零点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年在印度尼西亚日惹举办的亚洲乒乓球锦标赛男子团体决赛中，中国队与韩国队相遇，中国队男子选手A，B，C，D，E依次出场比赛，在以往对战韩国选手的比赛中他们五人获胜的概率分别是0.8，0.8，0.8，0.75，0.7，并且比赛胜负相互独立.赛会釆用5局3胜制，先赢3局者获得胜利.

    （1）在决赛中，中国队以3∶1获胜的概率是多少？

    （2）求比赛局数的分布列及数学期望.

    查看答案和解析>>

    同步练习册答案