
【探究一】从每一个位置剪断绳子,都是一个基本事件,剪断位置可以是长度为3 m的绳子上的任意一点,基本事件有有限多个,而且每一个基本事件的发生都是等可能的,因此事件的发生的概率只与剪断位置所处的绳子的长度有关,符合几何概型的条件.
【解析】如图3-3-20,记A={剪得两段绳子都不小于1 m},把绳子三等分,于是当剪断位置处在中间一段上时,事件A发生.由于中间一段的长度为3×![]() =1 m,所以事件A发生的概率P(A)=
=1 m,所以事件A发生的概率P(A)=![]() .
.
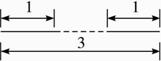
图3-3-20
【探究二】在任意位置剪断绳子,则剪断位置到一端点的距离取遍[0,3]内的任意数,并且每一个实数被取到都是等可能的.因此在任意位置剪断绳子的所有结果(基本事件)对应[0,3]上的均匀随机数,其中取得的[1,2]内的随机数就表示剪断位置与端点距离在[1,2]内,也就是剪得两段长都不小于1 m.这样取得的[1,2]内的随机数个数与[0,3]内的随机数个数之比就是事件A发生的概率.
【解法一】(1)利用计算器或计算机产生一组0到1区间的均匀随机数,a1=RAND.
(2)经过伸缩变换a=a1*3.
(3)统计出[1,2]内随机数的个数N1和[0,3]内随机数的个数N.
(4)计算频率fn(A)=![]() 即为概率P(A)的近似值.
即为概率P(A)的近似值.
【解法二】做一个带有指针的圆盘,把圆周三等分,标上刻度[0,3](这里3和0重合).转动圆盘记下指针指在[1,2](表示剪断绳子位置在[1,2]范围内)的次数N1及试验总次数N,则fn(A)= ![]() 即为概率P(A)的近似值.
即为概率P(A)的近似值.
规律总结 解法二用转盘产生随机数,这种方法可以亲自动手操作,但费时费力,试验次数不可能很大;解法一用计算机产生随机数,可以产生大量的随机数,又可以自动统计试验的结果,同时可以在短时间内多次重复试验,可以对试验结果的随机性和规律性有更深刻的认识.


科目:高中数学 来源:2014届广东省高二第二学期期中考试数学理试卷(解析版) 题型:填空题
取一根长度为3 m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1 m的概率是 。
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修3 3.3几何概型练习卷(二)(解析版) 题型:选择题
取一根长度为3 m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1 m的概率是.
A.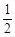 B.
B.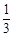 C.
C.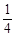 D.不确定
D.不确定
查看答案和解析>>
科目:高中数学 来源:陕西省2009-2010学年度高二第二学期期末考试数学试题(理科) 题型:选择题
取一根长度为3 m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1 m的概率是( )
A.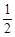 B.
B.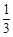 C.
C.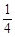 D.不确定
D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com