
分析 (1)利用an与Sn之间的关系、计算可知数列{an}构成首项、公比均为$\frac{1}{3}$的等比数列,进而计算可得结论;
(2)通过(1)可知log3an=-n,从而bn=-$\frac{n(n+1)}{2}$,裂项可知$\frac{1}{{b}_{n}}$=-2($\frac{1}{n}$-$\frac{1}{n+1}$),进而并项相加即得结论.
解答 解:(1)当n≥2时,an=Sn-Sn-1
=$\frac{{1-{a_n}}}{2}$-$\frac{1-{a}_{n-1}}{2}$,
整理得:an=$\frac{1}{3}$an-1,
当n=1时,a1=$\frac{1-{a}_{1}}{2}$,即a1=$\frac{1}{3}$,
∴数列{an}是首项、公比均为$\frac{1}{3}$的等比数列,
∴其通项公式an=$\frac{1}{{3}^{n}}$;
(2)由(1)可知log3an=log3$\frac{1}{{3}^{n}}$=-n,
∴bn=log3a1+log3a2+…+log3an
=-(1+2+…+n)
=-$\frac{n(n+1)}{2}$,
∴$\frac{1}{{b}_{n}}$=-$\frac{2}{n(n+1)}$=-2($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Tn=-2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=-2(1-$\frac{1}{n+1}$)
=-$\frac{2n}{n+1}$.
点评 本题考查数列的通项及前n项和,利用an与Sn之间的关系以及裂项、并项相加法是解决本题的关键,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
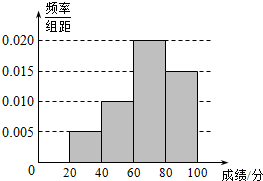 某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com