
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有5名男志愿![]() 和3名女志愿者
和3名女志愿者![]() ,从中随机抽取4人接受甲种心理暗示,另4人接受乙种心理暗示.
,从中随机抽取4人接受甲种心理暗示,另4人接受乙种心理暗示.
(1)求接受甲种心理暗示的志愿者中包含![]() 但不包含
但不包含![]() 的频率.
的频率.
(2)用![]() 表示接受乙种心理暗示的女志愿者人数,求
表示接受乙种心理暗示的女志愿者人数,求![]() 的分布列与数学期望
的分布列与数学期望![]()
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() ,
, ![]() )的一系列对应最值如表:
)的一系列对应最值如表:
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格提供的数据求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间和对称轴;
的单调递增区间和对称轴;
(3)若当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中, ![]() 是
是![]() 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
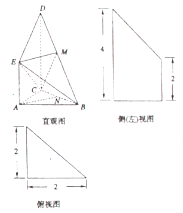
(1)求出该几何体的体积;
(2)若![]() 是
是![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,在以极点为直角坐标原点
,在以极点为直角坐标原点![]() ,极轴为
,极轴为![]() 轴的正半轴建立的平面直角坐标系
轴的正半轴建立的平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为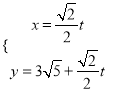 (
(![]() 为参数).
为参数).
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在平面直角坐标系中,设曲线![]() 经过伸缩变换
经过伸缩变换![]() :
:  得到曲线
得到曲线![]() ,若
,若![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是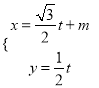 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在探究实系数一元二次方程的根与系数的关系时,可按下述方法进行:
设实系数一元二次方程![]() ……①
……①
在复数集![]() 内的根为
内的根为![]() ,
, ![]() ,则方程①可变形为
,则方程①可变形为![]() ,
,
展开得![]() .……②
.……②
比较①②可以得到: 
类比上述方法,设实系数一元![]() 次方程
次方程![]() (
(![]() 且
且![]() )在复数集
)在复数集![]() 内的根为
内的根为![]() ,
, ![]() ,…,
,…, ![]() ,则这
,则这![]() 个根的积
个根的积![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com