
已知正方体 棱长为1,点
棱长为1,点 在
在 上,且
上,且 ,点
,点 在平面
在平面 内,动点
内,动点 到直线
到直线 的距离与
的距离与 到点
到点 的距离的平方差等于1,则动点
的距离的平方差等于1,则动点 的轨迹是( )
的轨迹是( )
| A.圆 | B.抛物线 | C.双曲线 | D.直线 |
B
解析试题分析:作PN⊥AD,则PN⊥面A1D1DA,作 NH⊥A1D1 ,N,H为垂足则由三垂线定理可得 PH⊥A1D1.
以AB,AD,AA1 为x轴,y轴,z轴,建立空间坐标系,设P(x,y,0),由题意可得 M( ,0,0).
,0,0).
再由PN2+NH2=PH2,PH2-PM2=1,可得 PN2+NH2-PM2=1,
即 x2 +1-[(x-  )2+(y-0)2]=1,化简可得y2=
)2+(y-0)2]=1,化简可得y2=  x-
x-  ,故答案为B
,故答案为B
考点:本题主要是考查点轨迹方程的求法。属于中档题.
点评:解决该试题的关键是得到 x2+1-[(x-  )2+(y-0)2]=1,以AB,AD,AA1 为x轴,y轴,z轴,建立空间坐标系,设P(x,y,0),由题意可得 M(
)2+(y-0)2]=1,以AB,AD,AA1 为x轴,y轴,z轴,建立空间坐标系,设P(x,y,0),由题意可得 M( ,0,0),由题意可得(y2+1)-[(x-
,0,0),由题意可得(y2+1)-[(x-  )2+(y-0)2]=1,化简可得结果.
)2+(y-0)2]=1,化简可得结果.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:单选题
利用斜二测画法得到的
①三角形的直观图一定是三角形; ②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形; ④菱形的直观图一定是菱形.
以上结论正确的是 ( )
| A.①② | B.① | C.③④ | D.①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,三棱柱A1B1C1—ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( ).
| A.AE、B1C1为异面直线,且AE⊥B1C1 |
| B.AC⊥平面A1B1BA |
| C.CC1与B1E是异面直线 |
| D.A1C1∥平面AB1E |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知三棱锥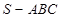 的所有顶点都在球O的表面上,三角形ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为( )
的所有顶点都在球O的表面上,三角形ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为 ( )
A. | B. | C. | D. |

查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,M、N、P为正方体AC1的棱AA1、A1B1、A1D1的中点,现沿截面MNP切去锥体A1-MNP,则剩余几何体的侧视图(左视图)为( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com