
【题目】2020年初,我国突发新冠肺炎疫情,疫情期间中小学生“停课不停学”.已知某地区中小学生人数情况如甲图所示,各学段学生在疫情期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与“家务劳动”的情况,现用分层抽样的方法抽取4%小学初中高中学段的学生进行调查,则抽取的样本容量、抽取的高中生家中参与“家务劳动”的人数分别为( )
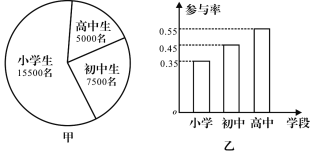
A.2750,200B.2750,110C.1120,110D.1120,200
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,曲线
,曲线![]() 上任意一点到
上任意一点到![]() 的距离等于该点到直线
的距离等于该点到直线![]() 的距离.
的距离.
(Ⅰ)求![]() 及曲线
及曲线![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆只有一个交点
与椭圆只有一个交点![]() ,与曲线
,与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,底面三角形
,底面三角形![]() 是正三角形,E是BC中点,则下列叙述正确的是( )
是正三角形,E是BC中点,则下列叙述正确的是( )

A.![]() 与
与![]() 是异面直线B.
是异面直线B.![]() 平面
平面![]()
C.AE,![]() 为异面直线,且
为异面直线,且![]() D.
D.![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春季,某出租汽车公同决定更换一批新的小汽车以代替原来报废的出租车,现有采购成本分别为11万元/辆和8万元/辆的A,B两款车型,根据以往这两种出租车车型的数据,得到两款出租车型使用寿命频数表如表:
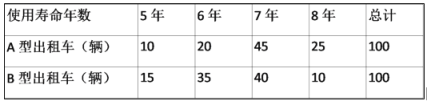
(1)填写如表,并判断是否有99%的把握认为出租车的使用寿命年数与汽车车有关?
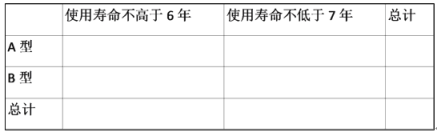
(2)以频率估计概率,从2020年生产的A和B的车型中各随机抽1车,以X表示这2车中使用寿命不低于7年的车数,求X的分布列和数学期望;
(3)根据公司要求,采购成本由出租公司负责,平均每辆出租每年上交公司6万元,其余维修和保险等费用自理,假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这100辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
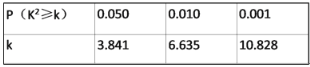
参考公式: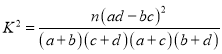 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,底面
中,底面![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
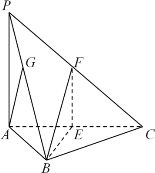
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系.每年交强险最终保险费计算方法是:交强险最终保险费![]() ,其中a为交强险基础保险费,A为与道路交通事故相联系的浮动比率,同时满足多个浮动因素的,按照向上浮动或者向下浮动比率的高者计算.按照我国《机动车交通事故责任强制保险基础费率表》的规定:普通6座以下私家车的交强险基础保险费
,其中a为交强险基础保险费,A为与道路交通事故相联系的浮动比率,同时满足多个浮动因素的,按照向上浮动或者向下浮动比率的高者计算.按照我国《机动车交通事故责任强制保险基础费率表》的规定:普通6座以下私家车的交强险基础保险费![]() 为950元,交强险费率浮动因素及比率如下表:
为950元,交强险费率浮动因素及比率如下表:
交强险浮动因素和浮动费率比率表 | ||
类型 | 浮动因素 | 浮动比率 |
| 上一个年度未发生有责任道路交通事故 |
|
| 上两个年度未发生有责任道路交通事故 |
|
| 上三个及以上年度未发生有责任道路交通事故 |
|
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及以上有责任道路交通事故 |
|
| 上一个年度发生有责任道路交通死亡事故 |
|
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了100辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计结果如下表:
类型 |
|
|
|
|
|
|
数量 | 25 | 10 | 10 | 25 | 20 | 10 |
以这100辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题.
(1)记X为一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望(数学期望值保留到个位数字);
(2)某二手车销售商专门销售这一品牌的二手车,且将经销商购车后下一年的交强险最终保险费高于交强险基础保险费![]() 的车辆记为事故车,假设购进一辆事故车亏损3000元,购进一辆非事故车盈利5000元.
的车辆记为事故车,假设购进一辆事故车亏损3000元,购进一辆非事故车盈利5000元.
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至少有一辆是事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线![]() 的参数方程为
的参数方程为 ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() 求直线
求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若把曲线
若把曲线![]() 上给点的横坐标伸长为原来的
上给点的横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的
倍,纵坐标伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且四个顶点构成的四边形的面积是
,且四个顶点构成的四边形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且不垂直于
,且不垂直于![]() 轴,直线
轴,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,直线
的中点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 是坐标原点),若四边形
是坐标原点),若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
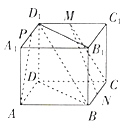
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;②AP,CM,DD1相交于一点;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正确结论的编号是( )
A.①④B.②④C.①④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com