
分析 设AB、AC上分别有点D、E满足AD=$\frac{2}{3}$AB,且AE=$\frac{2}{3}$AC,可得△ADE∽△ABC,且相似比为$\frac{2}{3}$.根据题意,当P在△ADE内运动时,△PBC的面积大于△ABC面积的$\frac{1}{3}$,由此结合相似三角形的性质和几何概型计算公式即可得到本题的概率.
解答 解:设AB、AC上分别有点D、E满足AD=$\frac{2}{3}$AB,且AE=$\frac{2}{3}$AC
∴△ADE∽△ABC,∴DE∥BC,且DE=$\frac{2}{3}$BC,
∵A到DE的距离等于A到BC距离的$\frac{2}{3}$,
∴DE到BC的距离等于△ABC高的$\frac{1}{3}$,
当动点P在△ABC内部运动,且在△ADE内时,P到BC的距离大于DE到BC的距离,
因此,当P在△ADE内运动时,△PBC的面积大于△ABC面积的$\frac{S}{3}$,
∴△PBC的面积大于$\frac{S}{3}$的概率是P=$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{2}{3}$)2=$\frac{4}{9}$.
故答案为:$\frac{4}{9}$.
点评 本题给出△ABC内部一点P,求△PBC的面积大于△ABC面积的$\frac{1}{3}$的概率.着重考查了相似三角形的性质和几何概型计算公式等知识,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
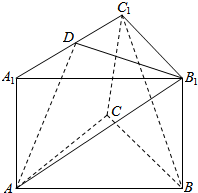 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,5) | B. | (1,7) | C. | ($\sqrt{7}$,7) | D. | ($\sqrt{7}$,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com