
分析 (Ⅰ)令$g(x)={e^x}-1-x,h(x)={e^x}-1-x-\frac{x^2}{2}$,g'(x)=ex-1.
分类讨论求解单调性,得出h(x)<h(0)=0,即可证明故${e^x}<1+x+\frac{x^2}{2}$.
(II)$f'(x)=2{e^2}+\frac{1}{x+1}-\frac{a}{10}≥0?a≤10({2{e^x}+\frac{1}{1+x}})$,
因此对一切x>-1有$a≤10({2{e^x}+\frac{1}{1+x}})$.构造函数t(x)=10(2ex+$\frac{1}{1+x}$),
求解导数$t'(x)=10({2{e^x}-\frac{1}{{{{(1+x)}^2}}}}),t''(x)=10({2{e^x}+\frac{1}{{{{(1+x)}^3}}}})>0$,
t'(x)在区间$({-\frac{1}{2},0})$上有唯一的零点,记它为x0,t(x0)>28.此28<t(x0)<28.9,
故整数a的最大值为28.
解答 解:(Ⅰ)令$g(x)={e^x}-1-x,h(x)={e^x}-1-x-\frac{x^2}{2}$,g'(x)=ex-1.
当x<0时,g'(x)<0,故g(x)在区间(-∞,0)上为减函数,
当x>0时,g'(x)>0,故g(x)在区间(0,+∞)上为增函数,
因此g(x)≥g(0)=0,故ex≥1+x.h'(x)=g(x)≥g(0)=0,因此h(x)为增函数,
当当x<0时,h(x)<h(0)=0,
故${e^x}<1+x+\frac{x^2}{2}$.
(Ⅱ)函数f(x)的定义域为(-1,+∞),
$f'(x)=2{e^2}+\frac{1}{x+1}-\frac{a}{10}≥0?a≤10({2{e^x}+\frac{1}{1+x}})$,
因此对一切x>-1有$a≤10({2{e^x}+\frac{1}{1+x}})$.
令t(x)=10(2ex+$\frac{1}{1+x}$)
则$t'(x)=10({2{e^x}-\frac{1}{{{{(1+x)}^2}}}}),t''(x)=10({2{e^x}+\frac{1}{{{{(1+x)}^3}}}})>0$,
故t'(x)为增函数,
又$t'({-\frac{1}{2}})=10({\frac{2}{{\sqrt{e}}}-4})<0,t'(0)=1>0$,
因此t'(x)在区间$({-\frac{1}{2},0})$上有唯一的零点,记它为x0,
不难知道t(x)min=t(x0),因此a≤t(x0).
由(Ⅰ)知ex≥1+x,
则$t(x)=10({2{e^x}+\frac{1}{1+x}})≥10[{2(1+x)+\frac{1}{1+x}}]≥20\sqrt{2}>28$,
因此t(x0)>28.
又$t({x_0})≤t(-0.2)=10({2{e^{-0.2}}+\frac{1}{1-0.2}})<10[{2({1-0.2+\frac{{{{0.2}^2}}}{2}})+\frac{1}{0.8}}]=28.9$,
因此28<t(x0)<28.9,
故整数a的最大值为28.
点评 本题综合考查了导数在解决不等式,函数单调性中的应用,学生的综合分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{13}$ | B. | $\frac{5}{7}$ | C. | $\frac{17}{25}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1)∪(-∞,-1) | C. | (-∞,1) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
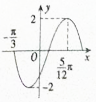 函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.
函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<0或0<x<$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com