
【题目】已知椭圆![]() 右焦点
右焦点![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是
是![]() 与
与![]() 在第一象限内的交点,且
在第一象限内的交点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知菱形![]() 的顶点
的顶点![]() 在椭圆
在椭圆![]() 上,顶点
上,顶点![]() 在直线
在直线![]() 上,求直线
上,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,过点
,过点![]() ,
,![]() 的直线与原点的距离为
的直线与原点的距离为![]() ,
,![]() 是椭圆上任一点,从原点
是椭圆上任一点,从原点![]() 向圆
向圆![]() :
:![]() 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点![]() ,
,![]() .
.
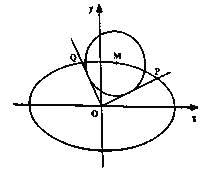
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
![]() 为定义在
为定义在![]() 上的“局部奇函数”;
上的“局部奇函数”;
![]() 曲线
曲线![]() 与
与![]() 轴交于不同的两点;
轴交于不同的两点;
若![]() 为假命题,
为假命题, ![]() 为真命题,求
为真命题,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次水下考古活动中,某一潜水员需潜水![]() 米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为
米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为![]() 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为![]() 升;②水底作业时间范围是最少
升;②水底作业时间范围是最少![]() 分钟最多
分钟最多![]() 分钟,每分钟用氧量为
分钟,每分钟用氧量为![]() 升;③返回水面时,平均速度为
升;③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为![]() 升.潜水员在此次考古活动中的总用氧量为
升.潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(1)如果水底作业时间是![]() 分钟,将
分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,水底作业时间为
,水底作业时间为![]() 分钟,求总用氧量
分钟,求总用氧量![]() 的取值范围;
的取值范围;
(3)若潜水员携带氧气![]() 升,请问潜水员最多在水下多少分钟(结果取整数)?
升,请问潜水员最多在水下多少分钟(结果取整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1、2、3、4、5的卡片,这5 张卡片除号码外完全相同.现进行有放回的连续抽取2 次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求事件“取出卡片号码之和不小于7 或小于5”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
, ![]() 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
(2)若![]() ,
, ![]() 都是从区间
都是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 成立的概率.
成立的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com