
| A. | 直角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
分析 利用三角恒等变换公式将公式变形,转化方向是变成简单的三角方程求角的值,通过角的值来确定△ABC的形状.
解答 证明:∵在△ABC中,sinC=$\frac{sinA+sinB}{cosA+cosB}$,
∴sin(A+B)=$\frac{2sin\frac{A+B}{2}cos\frac{A-B}{2}}{2cos\frac{A+B}{2}cos\frac{A-B}{2}}$,
∴2sin$\frac{A+B}{2}$cos$\frac{A+B}{2}$=$\frac{sin\frac{A+B}{2}}{cos\frac{A+B}{2}}$,
∴2cos2$\frac{A+B}{2}$-1=0,
∴cos(A+B)=0,
∴A+B=$\frac{π}{2}$,即C=$\frac{π}{2}$,
∴△ABC是直角三角形.
故选:A.
点评 考查利用三角恒等变换的公式进行灵活变形的能力,用来训练答题者掌握相关公式的熟练程度及选择变形方向的能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 182 | B. | 183 | C. | 184 | D. | 185 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
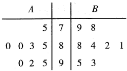 有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.
有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com