
ЁОЬтФПЁПШєЪ§Са{an}Тњзуa1ЃН1ЃЌa2ЃН1ЃЌan+2ЃНan+an+1ЃЌдђГЦЪ§Са{an}ЮЊьГВЈФЧЦѕЪ§СаЃЌьГВЈФЧЦѕТна§ЯпЪЧИљОньГВЈФЧЦѕЪ§СаЛГіРДЕФТна§ЧњЯпЃЌздШЛНчжаДцдкаэЖрьГВЈФЧЦѕТна§ЯпЕФЭМАИЃЌЪЧздШЛНчзюЭъУРЕФОЕфЛЦН№БШР§.зїЭМЙцдђЪЧдквдьГВЈФЧЦѕЪ§ЮЊБпЕФе§ЗНаЮЦДГЩЕФГЄЗНаЮжаЛвЛИідВаФНЧЮЊ90ЁуЕФЩШаЮЃЌСЌЦ№РДЕФЛЁЯпОЭЪЧьГВЈФЧЦѕТна§ЯпЃЌШчЭМЫљЪОЕФ7Иіе§ЗНаЮЕФБпГЄЗжБ№ЮЊa1ЃЌa2ЃЌЁЃЌa7ЃЌдкГЄЗНаЮABCDФкШЮШЁвЛЕуЃЌдђИУЕуВЛдкШЮКЮвЛИіЩШаЮФкЕФИХТЪЮЊЃЈ ЃЉ
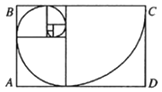
A.1![]() B.1
B.1![]() C.
C.![]() D.
D.![]()
 вЛЯпУћЪІЬсгХЪдОэЯЕСаД№АИ
вЛЯпУћЪІЬсгХЪдОэЯЕСаД№АИ бєЙтЪдОэЕЅдЊВтЪдОэЯЕСаД№АИ
бєЙтЪдОэЕЅдЊВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЮЊСЫСЫНтУёжкЖдПЊеЙДДНЈЮФУїГЧЪаЙЄзївдРДЕФТњвтЖШЃЌЫцЛњЕїВщСЫ40УћШКжкЃЌВЂНЋЫћУЧЫцЛњЗжГЩAЃЌBСНзщЃЌУПзщ20ШЫЃЌAзщШКжкИјЕквЛНзЖЮЕФДДЮФЙЄзїЦРЗжЃЌBзщШКжкИјЕкЖўНзЖЮЕФДДЮФЙЄзїЦРЗжЃЌИљОнСНзщШКжкЕФЦРЗжЛцжЦСЫШчЭМОЅвЖЭМЃК

![]() ИљОнОЅвЖЭМБШНЯШКжкЖдСНИіНзЖЮДДЮФЙЄзїТњвтЖШЦРЗжЕФЦНОљжЕМАМЏжаГЬЖШ
ИљОнОЅвЖЭМБШНЯШКжкЖдСНИіНзЖЮДДЮФЙЄзїТњвтЖШЦРЗжЕФЦНОљжЕМАМЏжаГЬЖШ![]() ВЛвЊЧѓМЦЫуГіОпЬхжЕЃЌИјГіНсТлМДПЩ
ВЛвЊЧѓМЦЫуГіОпЬхжЕЃЌИјГіНсТлМДПЩ![]() ЃЛ
ЃЛ
![]() ИљОнШКжкЕФЦРЗжНЋТњвтЖШДгЕЭЕНИпЗжЮЊШ§ИіЕШМЖЃК
ИљОнШКжкЕФЦРЗжНЋТњвтЖШДгЕЭЕНИпЗжЮЊШ§ИіЕШМЖЃК
ТњвтЖШЦРЗж | ЕЭгк70Зж | 70ЗжЕН89Зж | ВЛЕЭгк90Зж |
ТњвтЖШЕШМЖ | ВЛТњвт | Тњвт | ЗЧГЃТњвт |
![]() гЩЦЕТЪЙРМЦИХТЪЃЌХаЖЯИУЪаПЊеЙДДЮФЙЄзївдРДФФИіНзЖЮЕФУёжкТњвтТЪИпЃПЫЕУїРэгЩЃЎ
гЩЦЕТЪЙРМЦИХТЪЃЌХаЖЯИУЪаПЊеЙДДЮФЙЄзївдРДФФИіНзЖЮЕФУёжкТњвтТЪИпЃПЫЕУїРэгЩЃЎ
![]() ЭъГЩЯТУцЕФСаСЊБэЃЌВЂИљОнСаСЊБэХаЖЯЪЧЗёга
ЭъГЩЯТУцЕФСаСЊБэЃЌВЂИљОнСаСЊБэХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊУёжкЖдСНИіНзЖЮДДЮФЙЄзїЕФТњвтЖШДцдкВювьЃП
ЕФАбЮеШЯЮЊУёжкЖдСНИіНзЖЮДДЮФЙЄзїЕФТњвтЖШДцдкВювьЃП
ЕЭгк70Зж | ВЛЕЭгк70Зж | |
ЕквЛНзЖЮ | ||
ЕкЖўНзЖЮ |
ИНЃК![]()
|
|
|
|
k |
|
|
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙЪЙЌВЉЮядКЮхвЛЦкМфЭЌЪБОйАьЁАЯЗЧњЮФЛЏеЙЁБЁЂЁАУїДњгљНбДЩЦїеЙЁБЁЂЁАРњДњЧрТЬЩНЫЎЛеЙЁБЁЂ ЁАедУЯю\ЪщЛеЙЁБЫФИіеЙРРЃЎФГЭЌбЇОіЖЈдкЮхвЛЕБЬьЕФЩЯЁЂЯТЮчИїВЮЙлЦфжаЕФвЛИіЃЌЧвжСЩйВЮЙлвЛИіЛеЙЃЌдђВЛЭЌЕФВЮЙлЗНАИЙВга
A. 6жж B. 8жж C. 10жж D. 12жж
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]() .
.
ЃЈЂёЃЉШє![]() ЃЌЧѓКЏЪ§
ЃЌЧѓКЏЪ§![]() дк
дк![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈЂђЃЉЗНГЬ![]() га3ИіВЛЭЌЕФЪЕИљЃЌЧѓЪЕЪ§
га3ИіВЛЭЌЕФЪЕИљЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂѓЃЉЕБ![]() ЪБЃЌШєЖдгкШЮвтЕФ
ЪБЃЌШєЖдгкШЮвтЕФ![]() ЃЌЖМДцдк
ЃЌЖМДцдк![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌЧѓТњзуЬѕМўЕФе§ећЪ§
ЃЌЧѓТњзуЬѕМўЕФе§ећЪ§![]() ЕФШЁжЕЕФМЏКЯ.
ЕФШЁжЕЕФМЏКЯ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧњЯпCЕФВЮЪ§ЗНГЬЮЊ
жаЃЌЧњЯпCЕФВЮЪ§ЗНГЬЮЊ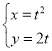 ЃЈtЮЊВЮЪ§ЃЉЃЌжБЯп
ЃЈtЮЊВЮЪ§ЃЉЃЌжБЯп![]() Й§Еу
Й§Еу![]() ЧвЧуаБНЧЮЊ
ЧвЧуаБНЧЮЊ![]() ЃЌвдзјБъдЕуOЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсЃЌШЁЯрЭЌЕФЕЅЮЛГЄЖШНЈСЂМЋзјБъЯЕ.
ЃЌвдзјБъдЕуOЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсЃЌШЁЯрЭЌЕФЕЅЮЛГЄЖШНЈСЂМЋзјБъЯЕ.
ЃЈ1ЃЉаДГіЧњЯпCЕФМЋзјБъЗНГЬКЭжБЯп![]() ЕФВЮЪ§ЗНГЬЃЛ
ЕФВЮЪ§ЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯпlгыЧњЯпCНЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНxexЃЌgЃЈxЃЉЃНaЃЈlnx+xЃЉ.
ЃЈ1ЃЉЕБaЃНeЪБЃЌЧѓжЄЃКfЃЈxЃЉЁнgЃЈxЃЉКуГЩСЂЃЛ
ЃЈ2ЃЉЕБaЃО0ЪБЃЌЧѓжЄЃКfЃЈxЃЉЁмgЃЈxЃЉ+1КугаНт.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЪЧЭждВ
ЪЧЭждВ![]() ЕФзѓгвЖЅЕуЃЌ
ЕФзѓгвЖЅЕуЃЌ![]() ЕуЮЊЭждВ
ЕуЮЊЭждВ![]() ЩЯвЛЕуЃЌЕу
ЩЯвЛЕуЃЌЕу![]() Йигк
Йигк![]() жсЕФЖдГЦЕуЮЊ
жсЕФЖдГЦЕуЮЊ![]() ЃЌЧв
ЃЌЧв![]() .
.
ЃЈ1ЃЉШєЭждВ![]() ОЙ§дВ
ОЙ§дВ![]() ЕФдВаФЃЌЧѓЭждВ
ЕФдВаФЃЌЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШєЙ§Еу![]() ЕФжБЯпгыЭждВ
ЕФжБЯпгыЭждВ![]() ЯрНЛгкВЛЭЌЕФ
ЯрНЛгкВЛЭЌЕФ![]() СНЕуЃЌЩш
СНЕуЃЌЩш![]() ЮЊЭждВ
ЮЊЭждВ![]() ЩЯвЛЕуЃЌЧвТњзу
ЩЯвЛЕуЃЌЧвТњзу![]() ЃЈ
ЃЈ![]() ЮЊзјБъдЕуЃЉЃЌЕБ
ЮЊзјБъдЕуЃЉЃЌЕБ![]() ЪБЃЌЧѓЪЕЪ§
ЪБЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЕФЖрУцЬхжаЃЌEAЁЭЦНУцABCЃЌDBЁЭЦНУцABCЃЌACЁЭBCЃЌCMЁЭABЃЌДЙзуЮЊMЃЌЧвAEЃНACЃН2![]() ЃЌBDЃН2BCЃН4ЃЌ
ЃЌBDЃН2BCЃН4ЃЌ
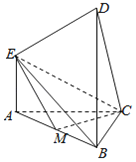
ЃЈ1ЃЉЧѓжЄЃКCMЁЭMEЃЛ
ЃЈ2ЃЉЧѓЖўУцНЧAЉMCЉEЕФгрЯвжЕЃЎ
ЃЈ3ЃЉдкЯпЖЮDCЩЯЪЧЗёДцдквЛЕуNЃЌЪЙЕУжБЯпBNЁЮЦНУцEMCЃЌШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬЃКдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЃК
ЃК![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌдквдЦНУцжБНЧзјБъЯЕЕФдЕуЮЊМЋЕуЁЂ
ЮЊВЮЪ§ЃЉЃЌдквдЦНУцжБНЧзјБъЯЕЕФдЕуЮЊМЋЕуЁЂ![]() жсЕФе§АыжсЮЊМЋжсЃЌЧвгыЦНУцжБНЧзјБъЯЕ
жсЕФе§АыжсЮЊМЋжсЃЌЧвгыЦНУцжБНЧзјБъЯЕ![]() ШЁЯрЭЌЕЅЮЛГЄЖШЕФМЋзјБъЯЕжаЃЌЧњЯп
ШЁЯрЭЌЕЅЮЛГЄЖШЕФМЋзјБъЯЕжаЃЌЧњЯп![]() ЃК
ЃК![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬвдМАЧњЯп
ЕФЦеЭЈЗНГЬвдМАЧњЯп![]() ЕФЦНУцжБНЧзјБъЗНГЬЃЛ
ЕФЦНУцжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉШєЧњЯп![]() ЩЯЧЁКУДцдкШ§ИіВЛЭЌЕФЕуЕНЧњЯп
ЩЯЧЁКУДцдкШ§ИіВЛЭЌЕФЕуЕНЧњЯп![]() ЕФОрРыЯрЕШЃЌЧѓетШ§ИіЕуЕФМЋзјБъ.
ЕФОрРыЯрЕШЃЌЧѓетШ§ИіЕуЕФМЋзјБъ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com