
| A. | 在[$\frac{π}{4}$,$\frac{π}{2}$]上是增函数 | |
| B. | 其图象关于直线x=-$\frac{π}{4}$对称 | |
| C. | 函数g(x)是奇函数 | |
| D. | 当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,函数g(x)的值域是[-2,1] |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,利用余弦函数的单调性、奇偶性、定义域和值域,以及它的图象的对称性,得出结论.
解答 解:函数f(x)=2sin(2x+$\frac{π}{6}$)的图象沿x轴向左平移$\frac{π}{6}$个长度单位,得到函数g(x)=2sin[2(x+$\frac{π}{6}$)+$\frac{π}{6}$]=2cos2x的图象,
对于函数g(x)=2cos2x,在[$\frac{π}{4}$,$\frac{π}{2}$]上,2x∈[$\frac{π}{2}$,π],g(x)为减函数,故排除A;
当x=-$\frac{π}{4}$时,g(x)=0,故g(x)的图象不关于直线x=-$\frac{π}{4}$对称,故排除B;
显然,g(x)为偶函数,故排除C;
当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,2x∈[$\frac{π}{3}$,$\frac{4π}{3}$],cos2x∈[-1,$\frac{1}{2}$],故函数g(x)的值域是[-2,1],故D正确,
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<f(b)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(a)<f(c) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,5) | B. | (-2,2) | C. | (-$\sqrt{7}$,$\sqrt{7}$) | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-3,1) | C. | (1,+∞) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 2或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
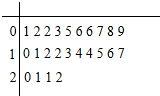 为调查了解某药物使用后病人的康复时间,从1000个使用该药的病人的康复时间中抽取了24个样本,数据如下图中的茎叶图(单位:周).专家指出康复时间在7周之内(含7周)是快效时间.
为调查了解某药物使用后病人的康复时间,从1000个使用该药的病人的康复时间中抽取了24个样本,数据如下图中的茎叶图(单位:周).专家指出康复时间在7周之内(含7周)是快效时间.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com