
【题目】设函数![]()
①若![]() ,则
,则![]() 的最大值为________;
的最大值为________;
②若函数![]() 有两个零点,则
有两个零点,则![]() 的取值范围是________.
的取值范围是________.
【答案】1 ![]()
【解析】
①,当a=0时,f(x)![]() ,由此分析函数的单调性,据此分析可得答案;
,由此分析函数的单调性,据此分析可得答案;
②,根据题意,由函数的解析式分析可得图象关于直线x=a对称,若函数y=f(x)﹣b有两个零点,即函数y=f(x)与y=b有2个交点,结合函数的图象分析可得答案.
解;①,当a=0时,f(x)![]() ,
,
当x≤0时,f(x)=2x,f(x)在(﹣∞,0]上为增函数,
当x>0时,﹣x<0,则f(x)=f(﹣x)=2﹣x=(![]() )x,
)x,
则f(x)在(0,+∞)为减函数,
则f(x)max=f(0)=20=1;
②,根据题意,当x≤a时,f(x)=2x﹣a,
当x>a时,则有2a﹣x<a,
此时f(x)=f(2a﹣x)=2a﹣x,
f(x)![]() ,其图象关于直线x=a对称,
,其图象关于直线x=a对称,
若函数y=f(x)﹣b有两个零点,即函数y=f(x)与y=b有2个交点,其图象如图:
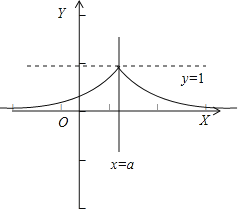
必有0<b<1,即b的取值范围为(0,1);
故答案为:①,1,②(0,1).


科目:高中数学 来源: 题型:
【题目】为了研究某种细菌的繁殖个数y随天数x的变化情况,收集数据如下:
天数x | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数y | 6 | 12 | 25 | 49 | 95 | 190 |
(1)根据散点图,判断![]() 与
与![]() 哪一个适合作为y关于x的回归方程类型;(给出判断即可,不用说明理由)
哪一个适合作为y关于x的回归方程类型;(给出判断即可,不用说明理由)
(2)根据(1)中的判断及表中数据,求y关于x的回归方程![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
参考公式: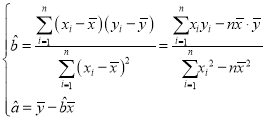
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B两种品牌各三种车型2017年7月的销量环比(与2017年6月比较)增长率如下表:
A品牌车型 | A1 | A2 | A3 | ||||
环比增长率 | -7.29% | 10.47% | 14.70% | ||||
B品牌车型 | B1 | B2 | B3 | ||||
环比增长率 | -8.49% | -28.06% | 13.25% | ||||
根据此表中的数据,有如下关于7月份销量的四个结论:①A1车型销量比B1车型销量多;
②A品牌三种车型总销量环比增长率可能大于14.70%;
③B品牌三款车型总销量环比增长率可能为正;
④A品牌三种车型总销量环比增长率可能小于B品牌三种车型总销量环比增长率.
其中正确结论的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左顶点为
,左顶点为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点,
两点,![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求证:直线![]() 恒过定点,并求出定点坐标.
恒过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=3x2-2x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com