
【题目】统计表明,某种型号的汽车在匀速行驶中每小时耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: ![]() ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
【答案】(1)17.5;(2)以80千米/小时的速度匀速行驶时耗油最少,最少为11.25升.
【解析】试题分析:(I)当![]() 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了![]() 小时,即可列出方程,求解结果;(II)当速度为
小时,即可列出方程,求解结果;(II)当速度为![]() 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了![]() 小时,设耗油量为
小时,设耗油量为![]() 升,根据题意列出函数关系式,利用导数得出函数的单调性,求解函数的最值,即可得到结论.
升,根据题意列出函数关系式,利用导数得出函数的单调性,求解函数的最值,即可得到结论.
试题解析:(I)当x=40时,汽车从甲地到乙地行驶了![]() 小时,
小时,
要耗没![]() (升).
(升).
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升
(II)当速度为![]() 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了![]() 小时,设耗油量为
小时,设耗油量为![]() 升,
升,
依题意得![]()
![]() 令
令![]() ,得
,得![]()
当![]() 时,
时, ![]() 是减函数;当
是减函数;当![]() 时,
时, ![]() 是增函数.
是增函数.
![]() 当
当![]() 时,
时, ![]() 取到极小值
取到极小值![]() 因为
因为![]() 在
在![]() 上只有一个极值,
上只有一个极值,
所以它是最小值.
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.


科目:高中数学 来源: 题型:
【题目】有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体的各条棱相切,第三个球过这个正方体的各个顶点,若正方体的棱长为![]() ,求这三个球的表面积.
,求这三个球的表面积.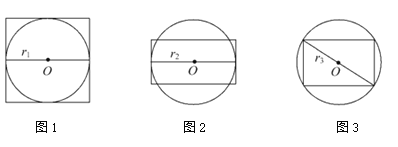
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切,设点
相切,设点![]() 为圆上一动点,
为圆上一动点, ![]() 轴于
轴于![]() ,且动点
,且动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)直线![]() 与直线
与直线![]() 垂直且与曲线
垂直且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() ,…,
,…, ![]() 是变量
是变量![]() 和
和![]() 的
的![]() 个样本点,直线
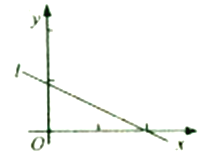
个样本点,直线![]() 是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )
是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )
A. ![]() 和
和![]() 的相关系数在
的相关系数在![]() 和
和![]() 之间
之间
B. ![]() 和
和![]() 的相关系数为直线
的相关系数为直线![]() 的斜率
的斜率
C. 当![]() 为偶数时,分布在
为偶数时,分布在![]() 两侧的样本点的个数一定相同
两侧的样本点的个数一定相同
D. 所有样本点![]() (
(![]() 1,2,…,
1,2,…, ![]() )都在直线
)都在直线![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图像如图所示,将
的部分图像如图所示,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.

(1)求函数![]() 的解析式;
的解析式;
(2)在![]() 中,角A,B,C满足
中,角A,B,C满足![]() ,且其外接圆的半径R=2,求
,且其外接圆的半径R=2,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
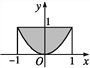
【题目】利用随机模拟方法计算y=x2与y=4围成的面积时,利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换,a=4a1-2,b=4b1,试验进行100次,前98次中落在所求面积区域内的样本点数为65,已知最后两次试验的随机数a1=0.3,b1=0.8及a1=0.4,b1=0.3,那么本次模拟得出的面积的近似值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com