练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】将编号的小球放入编号为的盒子中，要求不允许有空盒子，且球与盒子的号不能相同，则不同的放球方法有（ ）

    A. 16种 B. 12种 C. 9种 D. 6种

    【答案】B

    【解析】分析：利用分类讨论，求解每一种类型的放球方法数，然后利用分类加法计数原理求解即可．

    详解：由题意可知这四个小球有两个小球放在一个盒子中．

    当四个小球分组为如下情况时，放球方法有：

    当1与2号球放在同一盒子中时，有2种不同的放法；

    当1与3号球放在同一盒子中时，有2种不同的放法；

    当1与4号球放在同一盒子中时，有2种不同的放法；

    当2与3号球放在同一盒子中时，有2种不同的放法；

    当2与4号球放在同一盒子中时，有2种不同的放法；

    当3与4号球放在同一盒子中时，有2种不同的放法．

    综上可得不同的放球方法有12种．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】给出下列四个结论

    函数的最大值为；

    已知函数且在上是减函数，则a的取值范围是；

    在同一坐标系中，函数与的图象关于y轴对称；

    在同一坐标系中，函数与的图象关于直线对称．

    其中正确结论的序号是______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为增强学生体质,学校组织体育社团,某宿舍有4人积极报名参加篮球和足球社团,每人只能从两个社团中选择其中一个社团,大家约定:每个人通过掷一枚质地均匀的骰子决定自己参加哪个社团,掷出点数为5或6的人参加篮球社团,掷出点数小于5的人参加足球社团.

    (Ⅰ)求这4人中恰有1人参加篮球社团的概率；

    (Ⅱ)用分别表示这4人中参加篮球社团和足球社团的人数,记随机变量为和的乘积,求随机变量的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中，内角，，的对边，，满足

    （1）求的大小；

    （2）若， ，C角最小，求的面积S.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】十九大指出中国的电动汽车革命早已展开，通过以新能源汽车替代汽/柴油车，中国正在大力实施一项将重塑全球汽车行业的计划.年某企业计划引进新能源汽车生产设备，通过市场分析，全年需投入固定成本万元，每生产（百辆），需另投入成本万元，且.由市场调研知，每辆车售价万元，且全年内生产的车辆当年能全部销售完.

    （1）求出2018年的利润（万元）关于年产量（百辆）的函数关系式；（利润=销售额-成本）

    （2）2018年产量为多少百辆时，企业所获利润最大？并求出最大利润.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l：x+2y-2=0．试求：

    （1）点P（-2，-1）关于直线l的对称点坐标；

    （2）直线l关于点（1，1）对称的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，或，，．

    从以下两个命题中任选一个进行证明：

    当时函数恰有一个零点；

    当时函数恰有一个零点；

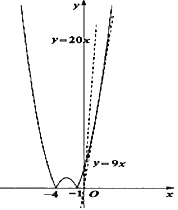
    如图所示当时如，与的图象“好像”只有一个交点，但实际上这两个函数有两个交点，请证明：当时，与两个交点．

    若方程恰有4个实数根，请结合的研究，指出实数k的取值范围不用证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    （1）当时，求的最小值；

    （2）若有三个不同的单调区间，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知立方和公式：

    求函数的值域；

    求函数，的值域；

    若任意实数x，不等式恒成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案